练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

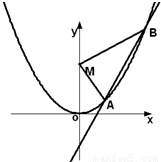
    如图，已知直线l：y＝2x＋m(m＜0)与抛物线C1：y＝ax2(a＞0)和圆C2：x2＋(y＋1)2＝5都相切，F是C1的焦点．

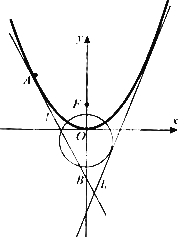
    (1)求m与a的值；

    (2)设A是C1上的一动点，以A为切点作抛物线C1的切线l，直线l交y轴于点B，以FA，FB为邻边作平行四边形FAMB，证明：点M在一条定直线上；

    (3)在(2)的条件下，记点M所在的定直线为l2，直线l2与y轴交点为N，连接MF交抛物线C1于P，Q两点，求△NPQ的面积S的取值范围．

    答案：
    解析：

    　　解：(1)，又

    　　　2分

    　　消去得：

    　　

    　　即　4分

    　　(2)设，切线的方程为　6分

    　　令，

    　　即　7分

    　　因此直线的方程为　8分

    　　令则

    　　点在直线　10分

    　　(3)设直线的方程为代入得：

    　　，　12分

    　　又　14分

    　　　14分


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    精英家教网如图，已知直线l：y=kx-2与抛物线C：x2=-2py（p＞0）交于A，B两点，O为坐标原点，
    OA
    +
    OB
    =(-4，-12)    ．
    （Ⅰ）求直线l和抛物线C的方程；
    （Ⅱ）抛物线上一动点P从A到B运动时，求△ABP面积最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

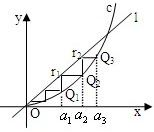    精英家教网设a＞0，如图，已知直线l：y=ax及曲线C：y=x2，C上的点Q1的横坐标为a1（0＜a1＜a）．从C上的点Qn（n≥1）作直线平行于x轴，交直线l于点Pn+1，再从点Pn+1作直线平行于y轴，交曲线C于点Qn+1．Qn（n=1，2，3，…）的横坐标构成数列{an}．
    （Ⅰ）试求an+1与an的关系，并求{an}的通项公式；
    （Ⅱ）当a=1，a1≤
    1
    2
    时，证明
    n
    k=1
    (ak-ak+1)ak+2＜
    1
    32
    ；
    （Ⅲ）当a=1时，证明
    n
    k-1
    (ak-ak+1)ak+2＜
    1
    3
    ．    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

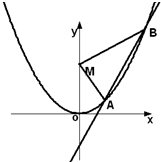    如图，已知直线L：y=kx-1与抛物线C：y=x2，相交于两点A、B，设点M（0，2），△MAB的面积为S．
    （1）若直线L上与M连线距离为1的点至多存在一个，求S的范围．
    （2）若直线L上与M连线的距离为1的点有两个，分别记为C、D，且满足S≥λ|CD|恒成立，求正数λ的范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

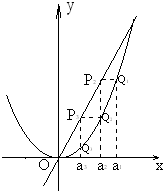    （2013•广州三模）如图，已知直线l：y=4x及曲线C：y=x2，C上的点Q1的横坐标为a1（0＜a1＜4）．从曲线C上的点Qn（n≥1）作直线平行于x轴，交直线l于点Pn+1，再从点Pn+1作直线平行于y轴，交曲线C于点Qn+1．Qn（n=1，2，3，…）的横坐标构成数列{an}．
    （1）试求an+1与an的关系； 
    （2）若曲线C的平行于直线l的切线的切点恰好介于点Q1，Q2之间（不与Q1，Q2重合），求a3的取值范围；
    （3）若a1=3，求数列{an}的通项公式．

    查看答案和解析>>

    科目：高中数学 来源：2012-2013学年浙江省温州市八校联考高三（上）期初数学试卷 （文科）（解析版） 题型：解答题

    如图，已知直线L：y=kx-1与抛物线C：y=x2，相交于两点A、B，设点M（0，2），△MAB的面积为S．
    （1）若直线L上与M连线距离为1的点至多存在一个，求S的范围．
    （2）若直线L上与M连线的距离为1的点有两个，分别记为C、D，且满足S≥λ|CD|恒成立，求正数λ的范围．

    查看答案和解析>>

    同步练习册答案