
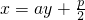 ,代入y2=2px,可得y2-2pay-p2=0(*),
,代入y2=2px,可得y2-2pay-p2=0(*), ,又y1y2=-4,所以-p2=-4,又p>0,可得p=2,
,又y1y2=-4,所以-p2=-4,又p>0,可得p=2,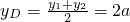 ,
,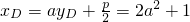 ,
, ,
,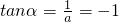 或-2,又α∈[0,π),
或-2,又α∈[0,π), 或π-arctan2.
或π-arctan2. 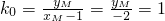 ,可得yM=-2,
,可得yM=-2,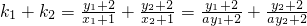 =
=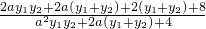 =
=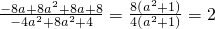 ,
,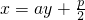 ,代入y2=2px,消掉x得y的二次方程,利用韦达定理及y1y2=-4即可求得p值,从而得抛物线方程;
,代入y2=2px,消掉x得y的二次方程,利用韦达定理及y1y2=-4即可求得p值,从而得抛物线方程; ,根据倾斜角范围即可求得α;
,根据倾斜角范围即可求得α;

 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:高中数学 来源: 题型:
| 3 |
| 2 |
| 3 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| n |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| d |
查看答案和解析>>
科目:高中数学 来源: 题型:
| OE |
| OA |
| OB |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com