
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是边长为
是边长为![]() 的正方形,侧面
的正方形,侧面![]()
底面![]() ,且
,且![]() ,
, ![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点.
的中点.

(1)求证: ![]() 平面
平面![]() ;
;
(2)求证:面![]() 平面
平面![]() ;
;
(3)在线段![]() 上是否存在点
上是否存在点![]() ,使得二面角
,使得二面角![]() 的余弦值为
的余弦值为![]() ?说明理由.
?说明理由.
【答案】(1)详见解析;(2)详见解析;(3)线段![]() 上存在点
上存在点![]() ,使得二面角
,使得二面角![]() 的余弦值为
的余弦值为![]() .
.
【解析】试题分析:(Ⅰ)连接AC,则F是AC的中点,E为PC 的中点,证明EF∥PA,留言在线与平面平行的判定定理证明EF∥平面PAD;
(Ⅱ)先证明CD⊥PA,然后证明PA⊥PD.利用直线与平面垂直的判定定理证明PA⊥平面PCD,最后根据面面垂直的判定定理即可得到面PAB⊥面PDC.
(Ⅲ)假设在线段AB上,存在点G,使得二面角C-PD-G的余弦值为![]() ,然后以O为原点,直线OA,OF,OP分别为x,y,z轴建立空间直角坐标系,设G(1,a,0)(0≤a≤2).利用空间向量的坐标运算求出a值,即可得出结论.
,然后以O为原点,直线OA,OF,OP分别为x,y,z轴建立空间直角坐标系,设G(1,a,0)(0≤a≤2).利用空间向量的坐标运算求出a值,即可得出结论.
试题解析:
(Ⅰ)证明:连结AC,由已知,F为AC的中点, ![]() 为
为![]() 中点.∴在
中点.∴在![]() 中,
中, ![]() //
// ![]()
且![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ∴
∴![]()
(Ⅱ)证明:因为平面![]() 平面
平面![]() , 平面
, 平面![]() 面
面![]()
![]() 为正方形,
为正方形, ![]() ,
, ![]() 平面
平面![]()
所以![]() 平面
平面![]() .
.
∴![]()
又![]() ,所以
,所以![]() 是等腰直角三角形, 且
是等腰直角三角形, 且![]() ,即
,即![]() .
.
![]() ,且
,且![]() 、
、![]() 面
面![]()
![]() 面
面![]()
又![]() 面
面![]() , ∴面
, ∴面![]() 面
面![]()
(Ⅲ)如图,
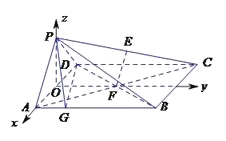
取![]() 的中点
的中点![]() ,连结
,连结![]() ,
, ![]() .
.
∵![]() ,∴
,∴![]() .
.
∵侧面![]() 底面
底面![]() ,
,
![]() ,
,
∴![]() ,
,
而![]() 分别为
分别为![]() 的中点,
的中点,
∴![]() ,又
,又![]() 是正方形,故
是正方形,故![]() .
.
∵![]() ,∴
,∴![]() ,
, ![]() .
.
以![]() 为原点,直线
为原点,直线![]() 分别为
分别为![]() 轴建立空间直角坐标系,
轴建立空间直角坐标系,
则有![]() ,
, ![]() ,
, ![]() .
.
若在![]() 上存在点
上存在点![]() 使得二面角
使得二面角![]() 的余弦值为
的余弦值为![]() ,连结
,连结![]()
设![]() .
.
由(Ⅱ)知平面![]() 的法向量为
的法向量为![]() .
.
设平面![]() 的法向量为
的法向量为![]() .∵
.∵![]() ,
,
∴由![]() 可得
可得![]() ,令
,令![]() ,则
,则![]() ,
,
故![]() ∴
∴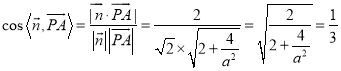 ,解得,
,解得, ![]() . 所以在线段
. 所以在线段![]() 上存在点
上存在点![]() ,使得二面角
,使得二面角![]() 的余弦值为
的余弦值为![]() ,此时
,此时![]() .
.


科目:高中数学 来源: 题型:
【题目】
如图,在四棱锥P—ABCD中,平面PAD⊥底面ABCD,其中底面ABCD为等腰梯形,AD∥BC,
PA=AB=BC=CD=2,PD=2![]() ,PA⊥PD,Q为PD的中点.
,PA⊥PD,Q为PD的中点.
(Ⅰ)证明:CQ∥平面PAB;
(Ⅱ)求三棱锥Q-ACD的体积。

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两位同学在高一年级的5次考试中,数学成绩统计如茎叶图所示,若甲、乙两人的平均成绩分别是 ![]() ,则下列叙述正确的是( )
,则下列叙述正确的是( ) 
A.![]() >
> ![]() ,乙比甲成绩稳定
,乙比甲成绩稳定
B.![]() >
> ![]() ,甲比乙成绩稳定
,甲比乙成绩稳定
C.![]() <
< ![]() ,乙比甲成绩稳定
,乙比甲成绩稳定
D.![]() <
< ![]() ,甲比乙成绩稳定
,甲比乙成绩稳定
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,OAB是一块半径为1,圆心角为 ![]() 的扇形空地.现决定在此空地上修建一个矩形的花坛CDEF,其中动点C在扇形的弧
的扇形空地.现决定在此空地上修建一个矩形的花坛CDEF,其中动点C在扇形的弧 ![]() 上,记∠COA=θ.
上,记∠COA=θ.
(Ⅰ)写出矩形CDEF的面积S与角θ之间的函数关系式;
(Ⅱ)当角θ取何值时,矩形CDEF的面积最大?并求出这个最大面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】园林管理处拟在公园某区域规划建设一半径为![]() 米圆心角为
米圆心角为![]() (弧度)的扇形景观水池,其中
(弧度)的扇形景观水池,其中![]() 为扇形
为扇形![]() 的圆心,同时紧贴水池周边建一圈理想的无宽度步道,要求总预算费用不超过
的圆心,同时紧贴水池周边建一圈理想的无宽度步道,要求总预算费用不超过![]() 万元,水池造价为每平方米
万元,水池造价为每平方米![]() 元,步道造价为每米
元,步道造价为每米![]() 元.
元.
(1)当![]() 和
和![]() 分别为多少时,可使广场面积最大,并求出最大值;
分别为多少时,可使广场面积最大,并求出最大值;
(2)若要求步道长为![]() 米,则可设计出水池最大面积是多少.
米,则可设计出水池最大面积是多少.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(cosx,cosx),
=(cosx,cosx), ![]() =(sinx,﹣cosx),记函数f(x)=2
=(sinx,﹣cosx),记函数f(x)=2 ![]()
![]() +1,其中x∈R.
+1,其中x∈R.
(Ⅰ)求函数f(x)的最小正周期及函数f(x)的图象的对称中心的坐标;
(Ⅱ)若α∈(0, ![]() ),且f(
),且f( ![]() )=
)= ![]() ,求cos2α的值.
,求cos2α的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知四棱锥P﹣ABCD中,PA⊥平面ABCD,底面ABCD是直角梯形, 且∠DAB=90°,∠ABC=45°,CB= ![]() ,AB=2,PA=1
,AB=2,PA=1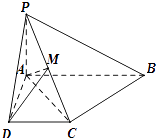
(1)求证:AB∥平面PCD;
(2)求证:BC⊥平面PAC;
(3)若M是PC的中点,求三棱锥C﹣MAD的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com