
| 3 |
| 4 |
| 4 |
| 5 |
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:山东省日照市2012届高三第一次模拟考试数学理科试题 题型:044
某校高二年级甲班有2名男乒乓球选手和3名女乒乓球选手,乙班有3名男乒乓球选手和1名乒乓球选手,学校计划从甲、乙两班各选2名选手参加体育交流活动.
(Ⅰ)求选出的4名选手均为男选手的概率.
(Ⅱ)若bn=an·log![]() an,数列{bn}的前n项和为Sn,求使sn+n·2n+1>50成立的正整数n的最小值.
an,数列{bn}的前n项和为Sn,求使sn+n·2n+1>50成立的正整数n的最小值.
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| 3 |
| 4 |
| 4 |
| 5 |
A.
| B.
| C.
| D.
|
查看答案和解析>>
科目:高中数学 来源: 题型:
为迎接北京奥运会的召开,某校高二年级准备举行“奥运礼仪知识”竞赛,要求每班选派2名同学参赛,2名同学都获奖的班级为获胜班级.高二(1)派男生甲和女生乙参赛,若甲获奖的概率为0.55,乙获奖的概率为0.6,甲、乙是否获奖互不影响.求:
(1)两人中只有1人获奖的概率;
(2)该班为获胜班级的概率.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年江西省吉安市高二(下)期末数学试卷(理科)(解析版) 题型:选择题
 和
和 ,现甲、乙各投篮一次,恰有一人投进球的概率是( )
,现甲、乙各投篮一次,恰有一人投进球的概率是( )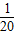
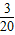

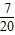
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com