
(本小题12分)如图,四边形ABCD是边长为1的正方形,MD⊥平面ABCD,NB⊥平面ABCD,且MD=NB=1,E是MN的中点。

(1)求证:平面AEC⊥平面AMN; (6分)
(2)求二面角M-AC-N的余弦值。 (6分)
(1)略
(2)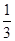
【解析】方法一、传统几何
(1)MD⊥平面ABCD,NB⊥平面ANCD,由直角三角形易得:AM=AN=MN=NC=MC=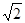 ,E是MN中点,可得AE⊥MN,CE⊥MN,又AE∩EC=E从而MN⊥平面AEC;
,E是MN中点,可得AE⊥MN,CE⊥MN,又AE∩EC=E从而MN⊥平面AEC;
(2)这里也有多种方法:
连接BD交AC与点O,底面是正方形得AC⊥BD,OE//MD推得OE⊥AC,得AC⊥平面MDBN,所以∠MON就是二面角M-AC-N的平面角,在矩形MDBN中根据长度可以求得cos∠MON=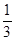 。
。

(亦可把二面角M-AC-N,拆成两个二面角M-AC-E和E-AC-N;或者抽取出正四面体MNAC,再求侧面与地面所成角;或者求平面ACN的垂线MB和平面ACM的垂线DN之间的夹角)
方法二、向量几何
MD⊥平面ABCD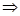 MD⊥DA,MD⊥DC,又底面ABCD为正方形
MD⊥DA,MD⊥DC,又底面ABCD为正方形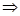 DA⊥DC,故以点D为坐标原点,DA为x轴,DC为y轴,DM为z轴,如图建立空间直角坐标系。
DA⊥DC,故以点D为坐标原点,DA为x轴,DC为y轴,DM为z轴,如图建立空间直角坐标系。
则各点的坐标A(1,0,0),B(1,1,0),C(0,1,0),M(0,0,1),N(1,1,1),
E( ,
, ,1)
……3分
,1)
……3分
(1) 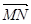 ·
·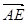 =…=0
=…=0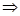 MN⊥AE;
MN⊥AE;
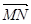 ·
·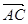 =…=0
=…=0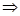 MN⊥AC
MN⊥AC
又AC∩AE=E,故MN⊥平面AEC; ………7分
(2)不妨设平面AMC的法向量为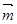 =(1,y,z),平面ANC的法向量为
=(1,y,z),平面ANC的法向量为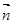 =(1,m,n) 则由
=(1,m,n) 则由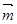 ⊥
⊥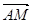 ,
,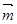 ⊥
⊥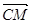
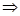
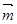 ·
·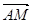 =0,
=0,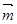 ·
·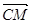 =0,代入坐标解得
=0,代入坐标解得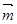 =(1,1,1)---9分
=(1,1,1)---9分
由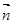 ⊥
⊥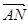 ,
,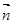 ⊥
⊥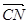
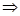
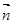 ·
·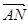 =0,
=0,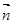 ·
·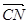 =0,代入坐标运算得
=0,代入坐标运算得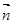 =(1,1,-1)--11分
=(1,1,-1)--11分
Cos<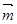 ,
,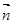 >=
>=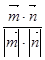 =
=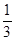 -------12分
-------12分


科目:高中数学 来源:2010-2011学年湖南省常德市高三质量检测考试数学理卷 题型:解答题
(本小题12分)
如图3,已知在侧棱垂直于底面
的三棱柱 中,AC=BC, AC⊥BC,点D是A1B1中点.
中,AC=BC, AC⊥BC,点D是A1B1中点.
(1)求证:平面AC1D⊥平面A1ABB1;
(2)若AC1与平面A1ABB1所成角的正弦值
为 ,求二面角D- AC1-A1的余弦值.
,求二面角D- AC1-A1的余弦值.

查看答案和解析>>
科目:高中数学 来源:2010-2011学年河北省高三高考压轴模拟考试文数 题型:解答题
(本小题12分)如图,四棱锥 中,
中,
侧面 是边长为2的正三角形,且与底面垂直,底面
是边长为2的正三角形,且与底面垂直,底面 是
是 的菱形,
的菱形, 为
为 的中点.
的中点.
(1)求 与底面
与底面 所成角的大小;
所成角的大小;
(2)求证: 平面
平面 ;
;
(3)求二面角 的余弦值.
的余弦值.

查看答案和解析>>
科目:高中数学 来源:2014届海南省高一上学期教学质量监测三数学 题型:解答题
(本小题12分)如图,四棱锥 中,底面
中,底面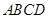 是正方形,
是正方形, ,
,  底面
底面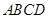 ,
,  分别在
分别在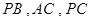 上,且
上,且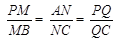
(1)求证:平面 ∥平面
∥平面 .
.
(2)求直线 与平面面
与平面面 所成角的正弦值.
所成角的正弦值.

查看答案和解析>>
科目:高中数学 来源:2010-2011年海南省高二下学期质量检测数学文卷(一) 题型:解答题
(本小题12分)
如图:⊙O为△ABC的外接圆,AB=AC,过点A的直线交⊙O于D,交BC延长线于F,DE是BD的延长线,连接CD。
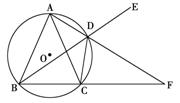
① 求证:∠EDF=∠CDF;
②求证:AB2=AF·AD。
查看答案和解析>>
科目:高中数学 来源:2009-2010集宁一中学高三年级理科数学第一学期期末考试试题 题型:解答题
(本小题12分)如图,四面体ABCD中,O、E分别是BD、BC的中点,

(I)求证: 平面BCD;
平面BCD;
(II)求异面直线AB与CD所成角的大小;
(III)求点E到平面ACD的距离。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com