
 (θ为参数,r>0)与曲线C2:
(θ为参数,r>0)与曲线C2: (t为参数)有公共点,则r的取值范围是 .
(t为参数)有公共点,则r的取值范围是 .  亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:高中数学 来源: 题型:
|
| 3π |
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
已知曲线C1:![]() (
(![]() 为参数),曲线C2:
为参数),曲线C2: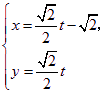 (t为参数).
(t为参数).
(Ⅰ)指出C1,C2各是什么曲线,并说明C1与C2公共点的个数;
(Ⅱ)若把C1,C2上各点的纵坐标都压缩为原来的一半,分别得到曲线![]() .写出
.写出![]() 的参数方程.
的参数方程.![]() 与
与![]() 公共点的个数和C
公共点的个数和C![]() 公共点的个数是否相同?说明你的理由.
公共点的个数是否相同?说明你的理由.
查看答案和解析>>
科目:高中数学 来源:2008年普通高等学校招生全国统一考试理科数学(宁夏卷) 题型:解答题
已知曲线C1: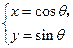 (
(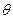 为参数),曲线C2:
为参数),曲线C2: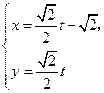 (t为参数).
(t为参数).
(Ⅰ)指出C1,C2各是什么曲线,并说明C1与C2公共点的个数;
(Ⅱ)若把C1,C2上各点的纵坐标都压缩为原来的一半,分别得到曲线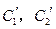 .写出
.写出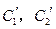 的参数方程.
的参数方程.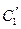 与
与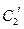 公共点的个数和C
公共点的个数和C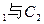 公共点的个数是否相同?说明你的理由.
公共点的个数是否相同?说明你的理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com