
【题目】在△ABC中,内角A,B,C的对边分别为a,b,c,已知![]()
(1)求![]() 的值
的值
(2)若![]() ,b=2,求△ABC的面积S.
,b=2,求△ABC的面积S.
【答案】(1)![]() ;(2)
;(2)![]() 。
。
【解析】
试题分析:(1)根据正弦定理变形![]() ,
,![]() ,
,![]() ,已知条件可转化为
,已知条件可转化为![]() ,即
,即![]() ,整理得:
,整理得:![]() ,根据和角公式,化为
,根据和角公式,化为![]() ,根据三角形内角和为
,根据三角形内角和为![]() 及诱导公式,可以得到
及诱导公式,可以得到![]() ,所以
,所以![]() ;(2)由正弦定理变形及第(1)问
;(2)由正弦定理变形及第(1)问![]() 可知,
可知,![]() ,根据余弦定理:
,根据余弦定理:![]() ,所以
,所以![]() ,又
,又![]() ,所以有
,所以有![]() ,解得
,解得![]() ,所以
,所以![]() ,
,![]() ,根据同角三角函数基本关系式由
,根据同角三角函数基本关系式由![]() 可知
可知![]() ,所以三角形面积为
,所以三角形面积为![]() 。
。
试题解析:(1)由正弦定理,则![]() =
=![]() ,所以
,所以![]() =
=![]() ,
,
即(cosA-2cosC)sinB=(2sinC-sinA)cosB,化简可得sin(A+B)=2sin(B+C).
因为A+B+C=π,所以sinC=2sinA.
因此![]()
(2)由![]() =2,得c=2a,由余弦定理b2=a2+c2-2accosB及cosB=
=2,得c=2a,由余弦定理b2=a2+c2-2accosB及cosB=![]() ,b=2,
,b=2,
得4=a2+4a2-4a2×![]() .解得a=1,从而c=2.
.解得a=1,从而c=2.
因为cosB=![]() ,所以sinB=
,所以sinB=![]() ,
,
因此S=![]() acsinB=
acsinB=![]() ×1×2×
×1×2×![]() =
=![]() .
.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:高中数学 来源: 题型:
【题目】若pVq是假命题,则( )
A. p,q至少有一个是假命题 B. p,q 均为假命题
C. p,q中恰有一个是假命题 D. p,q至少有一个是真命题
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】曲线f(x)=x3+x﹣2在p0处的切线平行于直线y=4x﹣1,则p0的坐标为( )
A. (1,0) B. (2,8)
C. (1,0)或(﹣1,﹣4) D. (2,8)或(﹣1,﹣4)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来我国电子商务行业迎来发展的新机遇.2016年“618”期间,某购物平台的销售业绩高达516亿元人民币.与此同时,相关管理部门推出了针对电商的商品和服务的评价体系.现从评价系统中选出200次成功交易,并对其评价进行统计,对商品的好评率为0.6,对服务的好评率为0.75,其中对商品和服务都做出好评的交易为80次.
(1)选完成关于商品和服务评价的![]() 列联表,再判断能否在犯错误的概率不超过0.001的前提下,认为商品好评与服务好评有关?
列联表,再判断能否在犯错误的概率不超过0.001的前提下,认为商品好评与服务好评有关?
(2)若将频率视为概率,某人在该购物平台上进行的3次购物中,设对商品和服务全为好评的次数为随机变量![]() :
:
①求对商品和服务全为好评的次数![]() 的分布列;
的分布列;
②求![]() 的数学期望和方差.
的数学期望和方差.
附临界值表:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
![]() 的观测值:
的观测值: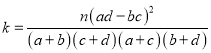 (其中
(其中![]() )关于商品和服务评价的
)关于商品和服务评价的![]() 列联表:
列联表:
对服务好评 | 对服务不满意 | 合计 | |
对商品好评 | 80 | ||
对商品不满意 | 10 | ||
合计 | 200 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某租赁公司拥有汽车100辆,当每辆车的月租金为3000元时,可全部租出;当每辆车的月租金每增加50元时,未租出的车将会增加一辆,租出的车每辆每月需要维护费150元,未租出的车每辆每月需要维护费50元.
(1)当每辆车的月租金定为3600元时,能租出多少辆车?
(2)当每辆车的月租金为多少元时,租赁公司的月收益最大?最大收益为多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)已知椭圆![]() 短轴的两个顶点与右焦点的连线构成等边三角形,直线
短轴的两个顶点与右焦点的连线构成等边三角形,直线![]() 与圆
与圆![]() 相切.
相切.
(1)求椭圆![]() 的方程;
的方程;
(2)已知椭圆![]() 的左顶点
的左顶点![]() 的两条直线
的两条直线![]() 分别交椭圆
分别交椭圆![]() 于
于![]() 两点,且
两点,且![]() ,求证:直线
,求证:直线![]() 过定点,并求出定点坐标;
过定点,并求出定点坐标;
(3)在(2)的条件下求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从孝感地区中小学生中抽取部分学生,进行肺活量调查.经了解,该地区小学、初中、高中三个学段学生的肺活量有较大差异,而同一学段男女生的肺活量差异不大.在下面的抽样方法中,最合理的抽样方法是( )
A. 简单的随机抽样 B. 按性别分层抽样 C. 按学段分层抽样 D. 系统抽样
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com