过抛物线y2=4x的焦点,作直线与抛物线相交于P、Q两点,求线段PQ中点的轨迹方程.
【答案】
分析:确定y
2=4x的焦点坐标,分类讨论,利用点差法,即可求得结论.
解答:解:∵y
2=4x的焦点坐标为F(1,0)
∴当直线PQ的斜率k存在时,可设其方程的y=k(x-1),且k≠0
又设P(x
1,y
1),Q(x
2,y
2),中点M的坐标为(x
,y
),则有:
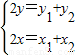
而由题意,得
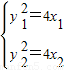
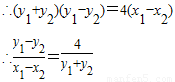
∴
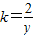
…(4分)
∵点M(x
,y
)在直线PQ上
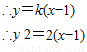
即得线段PQ中点的轨迹方程为y
2=2(x-1)…(5分)
而当直线PQ的斜率不存在时,有PQ⊥x轴,此时PQ的中点M,即为焦点F(1,0),满足y
2=2(x-1)
综上,线段PQ中点的轨迹方程为y
2=2(x-1)…(6分)
点评:本题考查轨迹方程,考查分类讨论的数学思想,考查学生的计算能力,属于中档题.

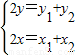
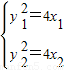
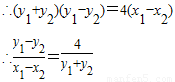
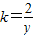 …(4分)
…(4分)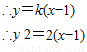


 名校课堂系列答案
名校课堂系列答案