解:(1)设动圆P的圆心坐标为P(x,y),
则由题意知:点N在圆M内,故圆M,P相内切,
∴|PM|=4-|PN|?|PM|+|PN|=4|MN|=
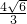
<4,
所以,动圆圆心P的轨迹是以M、N为焦点,长轴长为4的椭圆;
所以,动点P的轨迹方程为,
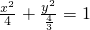
.
(2):

∴OA⊥OB,由对称性知,∠AOD=∠BOD=45°,
所以,直线OA的斜率k
OA=1,直线OA的方程为y=x,
由
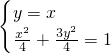
,得A(1,1);
又点A在圆D:(x-t)
2+y
2=t
2(t>0)上,
∴(1-t)
2+1=t
2,解得t=1.
(3):由

知,D是线段EF的中点,
不妨设E(x
1,y
1),由(2)知,D(1,0)∴F(2-x
1,-y
1)
设T(x
0,y
0),
则
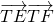
=(x
1-x
0,y
1-y
0)•(2-x
1-x
0,-y
1-y
0)
=(x
1-x
0)(2-x
1-x
0)+(y
1-y
0)(-y
1-y
0)
=2(x
1-x
0)-(x
12-x
02)+(y
02-y
12)
=-x
12+2x
1-y
12+x
02+y
02-2x
0=-[(x
1-1)
2+y
12]+1+x
02+y
02-2x
0=x
02-2x
0+

(1-
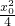
)
=

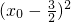
-

;
由-2≤x
0≤2知,当x
0=

时,
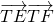
的最小值为-

;
分析:(1)先由点N在圆M内,得圆M,P相内切;有|PM|=4-|PN|?|PM|+|PN|=4|MN|=
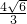
<4,可得动圆圆心P的轨迹是以M、N为焦点,长轴长为4的椭圆;即可求出动圆的圆心P的轨迹C的方程;
(2):

可得OA⊥OB,再由对称性知,∠AOD=∠BOD=45°,可以求得直线OA的方程为y=x,与椭圆方程联立可以求得点A的坐标;再利用点A在圆D代入即可求出实数t的值;
(3)先由

知,D是线段EF的中点,设出各点坐标,代入
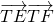
整理为一元二次函数,利用一元二次函数在固定区间上的最值求法即可求
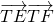
的最小值.
点评:本题主要考查向量在几何中的应用以及轨迹方程.第一问中的关键在于分析出圆M,P相内切;有|PM|=4-|PN|?|PM|+|PN|=4|MN|=
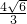
<4,进而得到动圆圆心P的轨迹是以M、N为焦点,长轴长为4的椭圆.

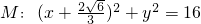 相切,且经过点
相切,且经过点 .
. ,请求出实数t的值;
,请求出实数t的值; ,点T是曲线C上的动点,试求
,点T是曲线C上的动点,试求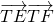 的最小值.
的最小值.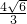 <4,
<4,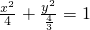 .
. ∴OA⊥OB,由对称性知,∠AOD=∠BOD=45°,
∴OA⊥OB,由对称性知,∠AOD=∠BOD=45°,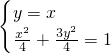 ,得A(1,1);
,得A(1,1); 知,D是线段EF的中点,
知,D是线段EF的中点,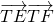 =(x1-x0,y1-y0)•(2-x1-x0,-y1-y0)
=(x1-x0,y1-y0)•(2-x1-x0,-y1-y0) (1-
(1-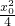 )
)
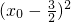 -
- ;
; 时,
时,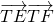 的最小值为-
的最小值为- ;
;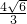 <4,可得动圆圆心P的轨迹是以M、N为焦点,长轴长为4的椭圆;即可求出动圆的圆心P的轨迹C的方程;
<4,可得动圆圆心P的轨迹是以M、N为焦点,长轴长为4的椭圆;即可求出动圆的圆心P的轨迹C的方程; 可得OA⊥OB,再由对称性知,∠AOD=∠BOD=45°,可以求得直线OA的方程为y=x,与椭圆方程联立可以求得点A的坐标;再利用点A在圆D代入即可求出实数t的值;
可得OA⊥OB,再由对称性知,∠AOD=∠BOD=45°,可以求得直线OA的方程为y=x,与椭圆方程联立可以求得点A的坐标;再利用点A在圆D代入即可求出实数t的值; 知,D是线段EF的中点,设出各点坐标,代入
知,D是线段EF的中点,设出各点坐标,代入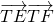 整理为一元二次函数,利用一元二次函数在固定区间上的最值求法即可求
整理为一元二次函数,利用一元二次函数在固定区间上的最值求法即可求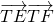 的最小值.
的最小值.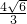 <4,进而得到动圆圆心P的轨迹是以M、N为焦点,长轴长为4的椭圆.
<4,进而得到动圆圆心P的轨迹是以M、N为焦点,长轴长为4的椭圆. 

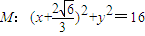 相切,且经过点
相切,且经过点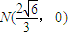 .
.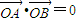 ,请求出实数t的值;
,请求出实数t的值;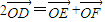 ,点T是曲线C上的动点,试求
,点T是曲线C上的动点,试求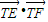 的最小值.
的最小值.