
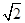 cosx(m>0)的最大值为2.
cosx(m>0)的最大值为2. 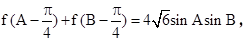 角A,B,C所对的边分别是a,b,c, 且C=60°,c=3,求△ABC的面积.
角A,B,C所对的边分别是a,b,c, 且C=60°,c=3,求△ABC的面积.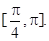 ; (2)
; (2)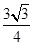 .
.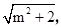 令其为2,即可求得m,利用正弦函数的单调性可求得此函数的递减区间,找到[0,π]上的单调递减区间即可;(2)本小题关键是求得边a与b的乘积,利用正弦定理,把
令其为2,即可求得m,利用正弦函数的单调性可求得此函数的递减区间,找到[0,π]上的单调递减区间即可;(2)本小题关键是求得边a与b的乘积,利用正弦定理,把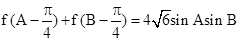 化为边a与b的关系,另一方面已知C=60°,c=3,由余弦定理,可得边a与b的另一关系,两式联立解得ab(当然也可解得a与b的单个值,但计算量大),利用
化为边a与b的关系,另一方面已知C=60°,c=3,由余弦定理,可得边a与b的另一关系,两式联立解得ab(当然也可解得a与b的单个值,但计算量大),利用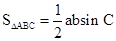 可求得面积.
可求得面积.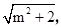 所以
所以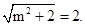 而m>0,于是m=
而m>0,于是m=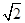 ,f(x)=2sin(x+
,f(x)=2sin(x+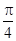 ).由正弦函数的单调性及周期性可得x满足
).由正弦函数的单调性及周期性可得x满足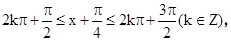 即
即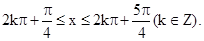 所以f(x)在[0,π]上的单调递减区间为
所以f(x)在[0,π]上的单调递减区间为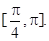
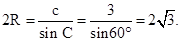 化简
化简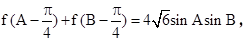 得sin A+sin B=2
得sin A+sin B=2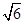 sin Asin B.由正弦定理,得
sin Asin B.由正弦定理,得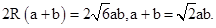 ① 由余弦定理,得a2+b2-ab=9,即(a+b)2-3ab-9="0." ②
① 由余弦定理,得a2+b2-ab=9,即(a+b)2-3ab-9="0." ②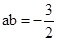 (舍去),故
(舍去),故
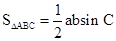 .
.

科目:高中数学 来源:不详 题型:解答题
| a |
| 3 |
| b |
| π |
| 2 |
| a |
| b |
| π |
| 2 |
| π |
| 2 |
| 14 |
| 5 |
| π |
| 4 |
| π |
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com