
 ,曲线
,曲线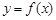 在点(2,
在点(2,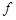 (2))处的切线方程为
(2))处的切线方程为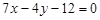
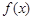 的解析式;
的解析式;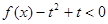 对一切
对一切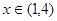 恒成立,求
恒成立,求 的取值范围;
的取值范围;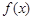 上任一点处的切线与直线
上任一点处的切线与直线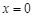 和直线
和直线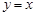 所围成的三角形面积为一值,并求此定值。
所围成的三角形面积为一值,并求此定值。 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:高中数学 来源:不详 题型:解答题
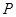 (元)与时间
(元)与时间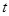 (天)所组成的有序数对
(天)所组成的有序数对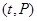 落在下图中的两条线段上,该股票在30天内的日交易量
落在下图中的两条线段上,该股票在30天内的日交易量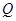 (万股)与时间
(万股)与时间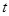 (天)的部分数据如下表所示.
(天)的部分数据如下表所示.
| 第t天 | 4 | 10 | 16 | 22 |
| Q(万股) | 36 | 30 | 24 | 18 |
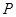 (元)与时间
(元)与时间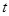 (天)所满足的函数关系式;
(天)所满足的函数关系式;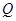 (万股)与时间
(万股)与时间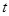 (天)的一次函数关系式;
(天)的一次函数关系式; (万元)表示该股票日交易额,写出
(万元)表示该股票日交易额,写出 关于
关于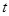 的函数关系式,并求这30天中第几天日交易额最大,最大值为多少?
的函数关系式,并求这30天中第几天日交易额最大,最大值为多少?查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 的图像先向右平移
的图像先向右平移 个单位,再向下平移两个单位,得到函数
个单位,再向下平移两个单位,得到函数 的图像.
的图像. 的表达式,并求出函数
的表达式,并求出函数 的表示式;
的表示式; 在
在 上的单调性和最大值;
上的单调性和最大值; ,
, ,问在
,问在 的图像上是否存在一点
的图像上是否存在一点 ,使得AP⊥BP
,使得AP⊥BP查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com