
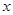 个月,顾客对某种商品的需求总量
个月,顾客对某种商品的需求总量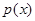 (单位:件)与
(单位:件)与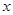 的关系近似地满足:
的关系近似地满足: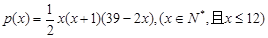 .该商品第
.该商品第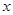 月的进货单价
月的进货单价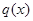 (单位:元)与x的近似关系是:
(单位:元)与x的近似关系是: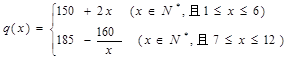
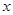 月的需求量
月的需求量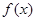 件与
件与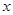 的函数关系式;
的函数关系式;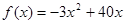
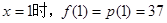 …………1分
…………1分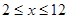 ,且
,且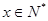 时,
时,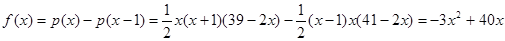 …………4分
…………4分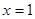 符合
符合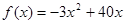 (x∈N*,且
(x∈N*,且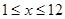 ). …………5分
). …………5分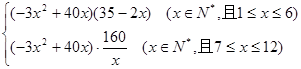
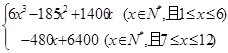
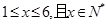 时
时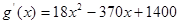 ,
,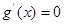 ,解得
,解得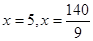 (舍去). …………9分
(舍去). …………9分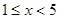 时,g′(x) >0,当
时,g′(x) >0,当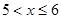 时,g′(x) <0,
时,g′(x) <0,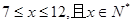 时,
时,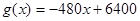 是减函数,
是减函数,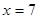 时,
时,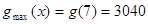 (元) …………13分
(元) …………13分

 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:高中数学 来源:不详 题型:解答题
 的正方形铁皮的四个角各截去一个边长为
的正方形铁皮的四个角各截去一个边长为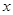 的小正方形,再将四边向上折起,做成一个无盖的长方体铁盒,且要求长方体的高度
的小正方形,再将四边向上折起,做成一个无盖的长方体铁盒,且要求长方体的高度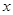 与底面正方形的边长的比不超过常数
与底面正方形的边长的比不超过常数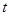 ,问:
,问: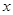 取何值时,长方体的容积V有最大值?
取何值时,长方体的容积V有最大值?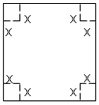
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com