解:(1)由已知得椭圆C的左顶点为A(-4,0),上顶点为D(0,2),
∴a=4,b=2,
故椭圆C的方程为

(2)直线AP的斜率k显然存在,且k>0,故可设直线AP的方程为y=k(x+4),从而M(5,9k),设P(x
0,y
0),则
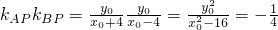
,∴直线BP的方程为:
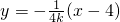
,
得

∴

当且仅当
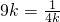
即

时等号成立
∴

时,线段MN的长度取最小值3.
(3)由(2)知,当线段MN的长度取最小值时,

,此时直线BP的方程为
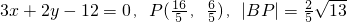
设与BP平行的直线l':3x+2y+t=0
联立
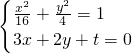
得10x
2+6tx+t
2-16=0
由△=36t
2-40(t
2-16)=0得

当
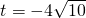
时,BP与l'的距离为
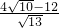
,此时S
△BPQ=
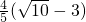
当

时,BP与l'的距离为
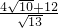
,此时S
△BPQ=
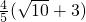
∴当

时,这样的Q点有4个
当
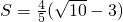
时,这样的Q点有3个
当
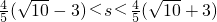
时,这样的Q点有2个
当
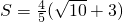
时,这样的Q点有1个
当

时,这样的Q点不存在.
分析:(1)由已知得,椭圆C的左顶点为A(-4,0),上顶点为D(0,2),由此能求出椭圆C的方程.
(2)线AP的斜率k显然存在,且k>0,故可设直线AP的方程为y=k(x+4),从而M(5,9k).由题设条件可以求出

,求得|MN|,再由均值不等式进行求解.
(3)由(2)知,当线段MN的长度取最小值时,

,设与BP平行的直线l':3x+2y+t=0
联立
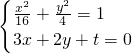
得10x
2+6tx+t
2-16=0,利用△=36t
2-40(t
2-16)=0得

最后即可解决问题.
点评:本题考查椭圆与直线的位置关系,(3)解答关系是利用方程的思想转化成根的判别等于0的问题,另外解题时要注意公式的灵活运用.

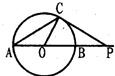
 的左顶点A和上顶点D,椭圆C的右顶点为B,点P是椭圆C上位于x轴上方的动点,直线AP,BP与直线l:x=5分别交于M,N两点.
的左顶点A和上顶点D,椭圆C的右顶点为B,点P是椭圆C上位于x轴上方的动点,直线AP,BP与直线l:x=5分别交于M,N两点.
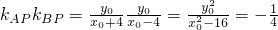 ,∴直线BP的方程为:
,∴直线BP的方程为: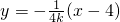 ,
,

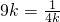 即
即 时等号成立
时等号成立 时,线段MN的长度取最小值3.
时,线段MN的长度取最小值3. ,此时直线BP的方程为
,此时直线BP的方程为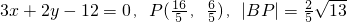
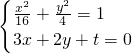 得10x2+6tx+t2-16=0
得10x2+6tx+t2-16=0
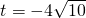 时,BP与l'的距离为
时,BP与l'的距离为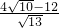 ,此时S△BPQ=
,此时S△BPQ=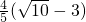
 时,BP与l'的距离为
时,BP与l'的距离为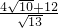 ,此时S△BPQ=
,此时S△BPQ=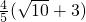
 时,这样的Q点有4个
时,这样的Q点有4个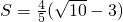 时,这样的Q点有3个
时,这样的Q点有3个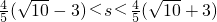 时,这样的Q点有2个
时,这样的Q点有2个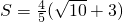 时,这样的Q点有1个
时,这样的Q点有1个 时,这样的Q点不存在.
时,这样的Q点不存在. ,求得|MN|,再由均值不等式进行求解.
,求得|MN|,再由均值不等式进行求解. ,设与BP平行的直线l':3x+2y+t=0
,设与BP平行的直线l':3x+2y+t=0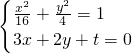 得10x2+6tx+t2-16=0,利用△=36t2-40(t2-16)=0得
得10x2+6tx+t2-16=0,利用△=36t2-40(t2-16)=0得 最后即可解决问题.
最后即可解决问题.

 选做题(考生只能从A、B、C题中选作一题)
选做题(考生只能从A、B、C题中选作一题) 选做题:(考生注意:请在下列三题中任选一题作答,如果多做,则按所做第一题评分)
选做题:(考生注意:请在下列三题中任选一题作答,如果多做,则按所做第一题评分)