
已知数列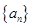 具有性质:①
具有性质:①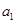 为整数;②对于任意的正整数
为整数;②对于任意的正整数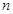 ,当
,当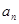 为偶数时,
为偶数时,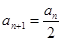 ;当
;当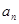 为奇数时,
为奇数时,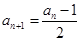 .
.
(1)若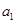 为偶数,且
为偶数,且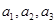 成等差数列,求
成等差数列,求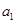 的值;
的值;
(2)设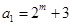 (
(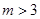 且
且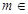 N),数列
N),数列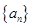 的前
的前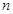 项和为
项和为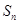 ,求证:
,求证: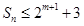 ;
;
(3)若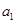 为正整数,求证:当
为正整数,求证:当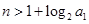 (
(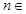 N)时,都有
N)时,都有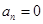 .
.
(1) 0或2;(2)证明见试题解析;(3)证明见试题解析.
【解析】
试题分析:(1)根据数列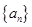 具有性质,
具有性质,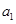 为偶数,
为偶数,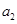
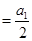 要,这时要求
要,这时要求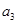 ,必须讨论
,必须讨论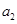 的奇偶性,分类讨论;(2)要证不等式
的奇偶性,分类讨论;(2)要证不等式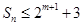 ,最好能求出
,最好能求出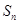 ,那么也就要求出数列
,那么也就要求出数列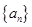 的各项,那么我们根据数列
的各项,那么我们根据数列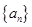 定义,由
定义,由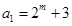 为奇数,则
为奇数,则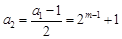 为奇数,
为奇数, 为偶数,接下来各项都是偶数,一起到某项为1,下面一项为0,以后全部为0.实际上项为1的项是第
为偶数,接下来各项都是偶数,一起到某项为1,下面一项为0,以后全部为0.实际上项为1的项是第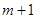 项(
项(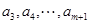 成等比数列),故
成等比数列),故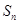 可求;(3)由于
可求;(3)由于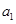 是正整数,要证明从某一项开始,数列各项均为0,这提示我们可首先证明
是正整数,要证明从某一项开始,数列各项均为0,这提示我们可首先证明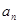 为非负(这可用数学归纳法加以证明),然后由于数列的关系,可见数列在出现0之前,是递减的,下面要考虑的是递减的速度而已.当
为非负(这可用数学归纳法加以证明),然后由于数列的关系,可见数列在出现0之前,是递减的,下面要考虑的是递减的速度而已.当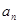 为偶数时,
为偶数时,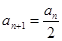 ;当
;当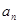 为奇数时,
为奇数时,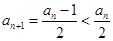 ,因此对所有正整数
,因此对所有正整数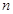 ,都有
,都有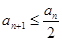 ,依此类推有
,依此类推有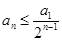 ,只要
,只要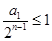 ,则有
,则有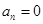 .
.
试题解析:(1)∵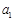 为偶数,∴可设
为偶数,∴可设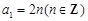 ,故
,故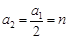 ,
,
若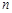 为偶数,则
为偶数,则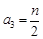 ,由
,由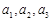 成等差数列,可知
成等差数列,可知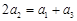 ,
,
即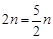 ,解得
,解得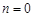 ,故
,故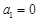 ; (2分)
; (2分)
若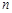 为奇数,则
为奇数,则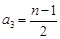 ,由
,由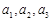 成等差数列,可知
成等差数列,可知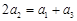 ,
,
即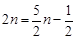 ,解得
,解得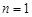 ,故
,故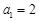 ;
;
∴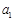 的值为0或2. (4分)
的值为0或2. (4分)
(2)∵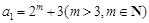 是奇数,∴
是奇数,∴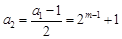 ,
,
 ,
,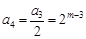 ,依此类推,
,依此类推,
可知 成等比数列,且有
成等比数列,且有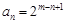
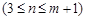 ,
,
又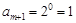 ,
,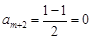 ,
,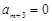 ,
,
∴当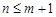 时,
时,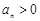 ;当
;当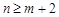 时,都有
时,都有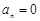 . (3分)
. (3分)
故对于给定的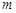 ,
,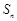 的最大值为
的最大值为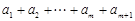
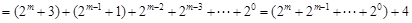
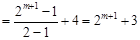 ,所以
,所以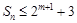 . (6分)
. (6分)
(3)当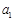 为正整数时,
为正整数时,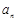 必为非负整数.证明如下:
必为非负整数.证明如下:
当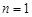 时,由已知
时,由已知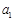 为正整数, 可知
为正整数, 可知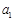 为非负整数,故结论成立;
为非负整数,故结论成立;
假设当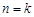 时,
时,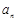 为非负整数,若
为非负整数,若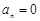 ,则
,则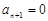 ;若
;若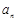 为正偶数,
为正偶数,
则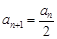 必为正整数;若
必为正整数;若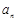 为正奇数,则
为正奇数,则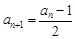 必为非负整数.
必为非负整数.
故总有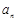 为非负整数. (3分)
为非负整数. (3分)
当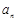 为奇数时,
为奇数时, 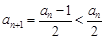 ;当
;当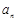 为偶数时,
为偶数时,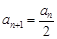 .
.
故总有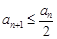 ,所以
,所以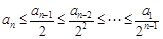 ,
,
当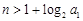 时,
时,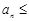
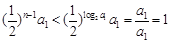 ,即
,即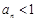 .( 6分)
.( 6分)
又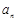 必为非负整数,故必有
必为非负整数,故必有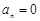 . (8分)
. (8分)
【另法提示:先证“若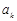 为整数,且
为整数,且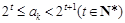 ,则
,则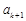 也为整数,且
也为整数,且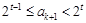 ”,然后由
”,然后由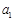 是正整数,可知存在正整数
是正整数,可知存在正整数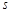 ,使得
,使得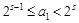 ,由此推得
,由此推得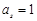 ,
,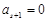 ,
,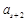 及其以后的项均为0,可得当
及其以后的项均为0,可得当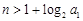
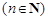 时,都有
时,都有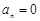 】
】
考点:(1)递推数列与等差数列;(2)数列的前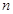 项和;(3)数列的通项与综合问题.
项和;(3)数列的通项与综合问题.


科目:高中数学 来源:2010年北京市海淀区高三一模理科试题 题型:单选题
已知数列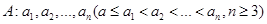 具有性质P:对任意
具有性质P:对任意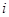 ,
,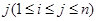 ,
,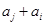 与
与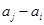 两数中至少有一个是该数列中的一项,现给出以下四个命题:
两数中至少有一个是该数列中的一项,现给出以下四个命题:
①数列0,1,3具有性质P;
②数列0,2,4,6具有性质P;
③若数列A具有性质P,则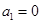 ;
;
④若数列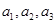
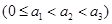 具有性质P,则
具有性质P,则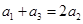
其中真命题有
| A.4个 | B.3个 | C.2个 | D.1个 |
查看答案和解析>>
科目:高中数学 来源:2013-2014学年上海市十二校高三12月联考文科数学试卷(解析版) 题型:解答题
已知数列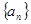 具有性质:①
具有性质:①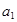 为正数;②对于任意的正整数
为正数;②对于任意的正整数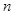 ,当
,当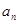 为偶数时,
为偶数时,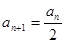 ;当
;当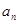 为奇数时,
为奇数时,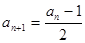
(1)若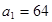 ,求数列
,求数列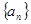 的通项公式;
的通项公式;
(2)若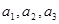 成等差数列,求
成等差数列,求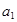 的值;
的值;
(3)设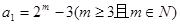 ,数列
,数列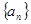 的前
的前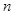 项和为
项和为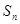 ,求证:
,求证: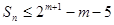
查看答案和解析>>
科目:高中数学 来源:2012-2013学年上海市黄浦区高三下学期二模数学试卷(解析版) 题型:解答题
已知数列 具有性质:①
具有性质:① 为整数;②对于任意的正整数
为整数;②对于任意的正整数 ,当
,当 为偶数时,
为偶数时,
 ;当
;当 为奇数时,
为奇数时, .
.
(1)若 为偶数,且
为偶数,且 成等差数列,求
成等差数列,求 的值;
的值;
(2)设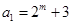 (
( 且
且 N),数列
N),数列 的前
的前 项和为
项和为 ,求证:
,求证: ;
;
(3)若 为正整数,求证:当
为正整数,求证:当 (
( N)时,都有
N)时,都有 .
.
查看答案和解析>>
科目:高中数学 来源:烟台市英文学校2010高三一模考试理科数学试题 题型:选择题
已知数列
具有性质P:对任意 ,
, ,
, 与
与
 两数中至少有一个是该数列中的一项,现给出
两数中至少有一个是该数列中的一项,现给出
以下四个命题:
①数列0,1,3具有性质P;
②数列0,2,4,6具有性质P;
③若数列A具有性质P,则 ;
;
④若数列
 具有性质P,则
具有性质P,则
其中真命题有 ( )
A.4个 B.3个 C.2个 D.1个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com