
已知数列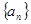 具有性质:①
具有性质:①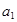 为正数;②对于任意的正整数
为正数;②对于任意的正整数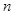 ,当
,当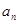 为偶数时,
为偶数时,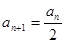 ;当
;当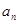 为奇数时,
为奇数时,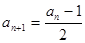
(1)若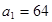 ,求数列
,求数列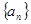 的通项公式;
的通项公式;
(2)若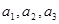 成等差数列,求
成等差数列,求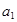 的值;
的值;
(3)设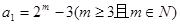 ,数列
,数列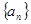 的前
的前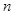 项和为
项和为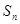 ,求证:
,求证: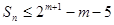
(1)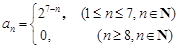 ;(2) 2;(3)证明见试题解析.
;(2) 2;(3)证明见试题解析.
【解析】
试题分析:(1)由于64不算大,可以依次计算出
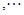 ,因为按照定义
,因为按照定义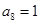 ,
,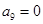 ,而此开始
,而此开始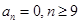 ,故可得出
,故可得出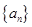 通项公式;(2)显然
通项公式;(2)显然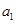 必须是整数,而且要计算
必须是整数,而且要计算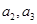 ,因此我们可以根据
,因此我们可以根据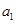 的值分类讨论(分成四类
的值分类讨论(分成四类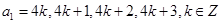 ).(3)
).(3)
要证不等式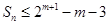 ,最好能求出
,最好能求出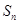 ,那么也就要求出数列
,那么也就要求出数列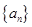 的各项,那么我们根据数列
的各项,那么我们根据数列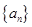 定义,由
定义,由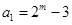 为奇数,则
为奇数,则 为偶数,
为偶数,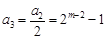 为奇数,接下来各项都是偶数,一起到某项为1,下面一项为0,以后全部为0.实际上项为1的项是第
为奇数,接下来各项都是偶数,一起到某项为1,下面一项为0,以后全部为0.实际上项为1的项是第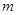 项,且
项,且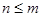 时
时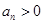 ,
,
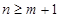 时
时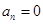 ,因此
,因此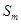 是最大的,但在计算
是最大的,但在计算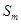 时,要注意当
时,要注意当 时,
时,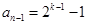 ,只要它不为0,就可继续下去.
,只要它不为0,就可继续下去.
试题解析:(1)由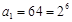 ,可得
,可得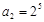 ,
,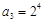 ,…,
,…,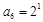 ,
,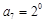 ,
,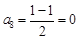 ,
,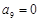 ,…,
,…,
即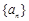 的前7项成等比数列,从第8起数列的项均为0. (2分)
的前7项成等比数列,从第8起数列的项均为0. (2分)
故数列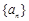 的通项公式为
的通项公式为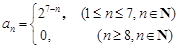 . (4分)
. (4分)
(2)若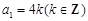 时,
时,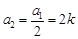 ,
,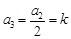 ,
,
由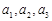 成等差数列,可知即
成等差数列,可知即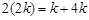 ,解得
,解得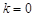 ,故
,故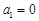 ;(舍去)
;(舍去)
若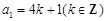 时,
时,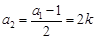 ,
,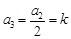 ,
,
由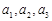 成等差数列,可知
成等差数列,可知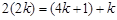 ,解得
,解得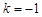 ,故
,故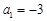 ;(舍去)(3分)
;(舍去)(3分)
若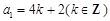 时,
时,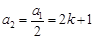 ,
,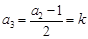 ,
,
由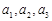 成等差数列,可知
成等差数列,可知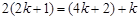 ,解得
,解得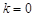 ,故
,故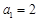 ;
;
若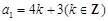 时,
时,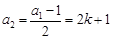 ,
,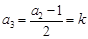 ,
,
由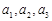 成等差数列,可知
成等差数列,可知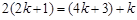 ,解得
,解得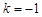 ,故
,故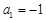 ;(舍去)
;(舍去)
∴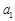 的值为2.
(6分)
的值为2.
(6分)
(3)由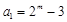 (
(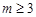 ),可得
),可得 ,
,
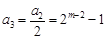 ,
,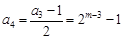 ,
,
若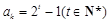 ,则
,则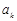 是奇数,从而
是奇数,从而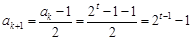 ,
,
可得当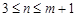 时,
时,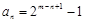 成立. (3分)
成立. (3分)
又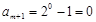 ,
,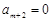 ,…
,…
故当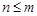 时,
时,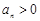 ;当
;当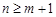 时,
时,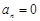 .
(5分)
.
(5分)
故对于给定的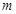 ,
,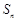 的最大值为
的最大值为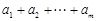
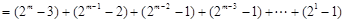
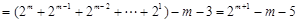 ,
,
故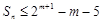 .
(8分)
.
(8分)
考点:(1)数列的通项公式(分段函数形式);(2)等差数列与分类讨论;(3)数列的前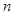 项和与最大值.
项和与最大值.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:2010年北京市海淀区高三一模理科试题 题型:单选题
已知数列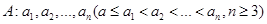 具有性质P:对任意
具有性质P:对任意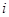 ,
,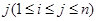 ,
,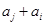 与
与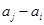 两数中至少有一个是该数列中的一项,现给出以下四个命题:
两数中至少有一个是该数列中的一项,现给出以下四个命题:
①数列0,1,3具有性质P;
②数列0,2,4,6具有性质P;
③若数列A具有性质P,则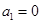 ;
;
④若数列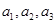
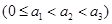 具有性质P,则
具有性质P,则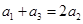
其中真命题有
| A.4个 | B.3个 | C.2个 | D.1个 |
查看答案和解析>>
科目:高中数学 来源:2013-2014学年上海市十二校高三12月联考理科数学试卷(解析版) 题型:解答题
已知数列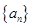 具有性质:①
具有性质:①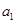 为整数;②对于任意的正整数
为整数;②对于任意的正整数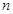 ,当
,当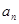 为偶数时,
为偶数时,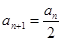 ;当
;当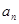 为奇数时,
为奇数时,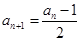 .
.
(1)若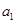 为偶数,且
为偶数,且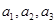 成等差数列,求
成等差数列,求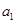 的值;
的值;
(2)设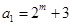 (
(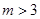 且
且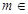 N),数列
N),数列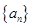 的前
的前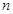 项和为
项和为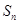 ,求证:
,求证: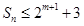 ;
;
(3)若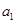 为正整数,求证:当
为正整数,求证:当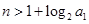 (
(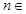 N)时,都有
N)时,都有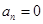 .
.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年上海市黄浦区高三下学期二模数学试卷(解析版) 题型:解答题
已知数列 具有性质:①
具有性质:① 为整数;②对于任意的正整数
为整数;②对于任意的正整数 ,当
,当 为偶数时,
为偶数时,
 ;当
;当 为奇数时,
为奇数时, .
.
(1)若 为偶数,且
为偶数,且 成等差数列,求
成等差数列,求 的值;
的值;
(2)设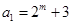 (
( 且
且 N),数列
N),数列 的前
的前 项和为
项和为 ,求证:
,求证: ;
;
(3)若 为正整数,求证:当
为正整数,求证:当 (
( N)时,都有
N)时,都有 .
.
查看答案和解析>>
科目:高中数学 来源:烟台市英文学校2010高三一模考试理科数学试题 题型:选择题
已知数列
具有性质P:对任意 ,
, ,
, 与
与
 两数中至少有一个是该数列中的一项,现给出
两数中至少有一个是该数列中的一项,现给出
以下四个命题:
①数列0,1,3具有性质P;
②数列0,2,4,6具有性质P;
③若数列A具有性质P,则 ;
;
④若数列
 具有性质P,则
具有性质P,则
其中真命题有 ( )
A.4个 B.3个 C.2个 D.1个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com