
【题目】已知抛物线![]() :
:![]() ,直线
,直线![]() :
:![]() .
.
(1)若直线![]() 与抛物线
与抛物线![]() 相切,求直线
相切,求直线![]() 的方程;
的方程;
(2)设![]() ,直线
,直线![]() 与抛物线
与抛物线![]() 交于不同的两点
交于不同的两点![]() ,
,![]() ,若存在点
,若存在点![]() ,满足
,满足![]() ,且线段
,且线段![]() 与
与![]() 互相平分(
互相平分(![]() 为原点),求
为原点),求![]() 的取值范围.
的取值范围.
【答案】(1)![]() (2)见解析
(2)见解析
【解析】
(1)联立直线方程与抛物线方程,利用![]() 即可求解。
即可求解。
(2)由直线与抛物线相交可得:![]() ,由(1)可得
,由(1)可得![]()
![]() ,由线段OC与AB互相平分可得四边形OACB为平行四边形,得到C
,由线段OC与AB互相平分可得四边形OACB为平行四边形,得到C![]() ,利用
,利用![]() 得到
得到![]() ,即:
,即:![]()
![]() =-1,再将
=-1,再将![]()
![]() ,
,![]() 代入即可求得
代入即可求得![]() ,对
,对![]() 的范围分类,利用基本不等式即可得解。
的范围分类,利用基本不等式即可得解。
解:(1)法1:由![]() 得
得![]()
![]()
所以,所求的切线方程为![]()
法2:因为直线![]() 恒过(0,-4),所以由
恒过(0,-4),所以由![]() 得
得![]()
设切点为![]() ,由题可得,直线与抛物线在
,由题可得,直线与抛物线在![]() 轴下方的图像相切,
轴下方的图像相切,
则![]()
所以切线方程为![]() ,将坐标(0,-4)代入得
,将坐标(0,-4)代入得![]()
即切点为(8,-8),再将该点代入![]() 得,
得,![]()
所以,所求的切线方程为![]()
(2)由![]() 得
得![]()
![]() 且
且![]() ,
,![]()
![]()
所以![]() ,
,
因为线段OC与AB互相平分,所以四边形OACB为平行四边形
![]()
![]() ,即C
,即C![]()
由![]() 得,
得,![]() ,
,
法1:所以![]()
![]() =-1
=-1
又![]()
 ,又
,又![]()
所以![]()
![]() ,所以
,所以![]()

法2:因为![]()
![]()
又![]()
![]() ,即
,即![]()



 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:高中数学 来源: 题型:
【题目】某公司有1000名员工,其中男性员工400名,采用分层抽样的方法随机抽取100名员工进行5G手机购买意向的调查,将计划在今年购买5G手机的员工称为“追光族",计划在明年及明年以后才购买5G手机的员工称为“观望者”,调查结果发现抽取的这100名员工中属于“追光族”的女性员工和男性员工各有20人.
(1)完成下列![]() 列联表,并判断是否有95%的把握认为该公司员工属于“追光族"与“性别"有关;
列联表,并判断是否有95%的把握认为该公司员工属于“追光族"与“性别"有关;
属于“追光族" | 属于“观望者" | 合计 | |
女性员工 | |||
男性员工 | |||
合计 | 100 |
(2)已知被抽取的这100名员工中有10名是人事部的员工,这10名中有3名属于“追光族”.现从这10名中随机抽取3名,记被抽取的3名中属于“追光族”的人数为随机变量X,求![]() 的分布列及数学期望.
的分布列及数学期望.
附 ,其中
,其中![]()
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法错误的是( )
A.命题“若![]() ,则
,则![]() ”的逆否命题为“若
”的逆否命题为“若![]() ,则
,则![]() ”
”
B.命题“![]() ,
,![]() ”是假命题
”是假命题
C.若命题![]() 、
、![]() 均为假命题,则命题
均为假命题,则命题![]() 为真命题
为真命题
D.若![]() 是定义在R上的函数,则“
是定义在R上的函数,则“![]() ”是“
”是“![]() 是奇函数”的必要不允分条件
是奇函数”的必要不允分条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】明初出现了一大批杰出的骑兵将领,比如徐达、常遇春、李文忠、蓝玉和朱棣.明初骑兵军团击败了不可一世的蒙古骑兵,是当时世界上最强骑兵军团.假设在明军与元军的某次战役中,明军有8位将领,善用骑兵的将领有5人;元军有8位将领,善用骑兵的有4人.
(1)现从明军将领中随机选取4名将领,求至多有3名是善用骑兵的将领的概率;
(2)在明军和元军的将领中各随机选取2人,![]() 为善用骑兵的将领的人数,写出
为善用骑兵的将领的人数,写出![]() 的分布列,并求
的分布列,并求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 是指大气中直径小于或等于2.5微米的颗粒物,也称为可吸入肺颗粒物.我国
是指大气中直径小于或等于2.5微米的颗粒物,也称为可吸入肺颗粒物.我国![]() 标准采用世卫组织设定的最宽限值,即
标准采用世卫组织设定的最宽限值,即![]() 日均值在35微克/立方米以下空气质量为一级;在35微克/立方米~75微克/立方米之间空气质量为二级;在75微克/立方米以上空气质量为超标.某试点城市环保局从该市市区2015年全年每天的
日均值在35微克/立方米以下空气质量为一级;在35微克/立方米~75微克/立方米之间空气质量为二级;在75微克/立方米以上空气质量为超标.某试点城市环保局从该市市区2015年全年每天的![]() 监测数据中随机抽取15天的数据作为样本,监测值如茎叶图所示(十位为茎,个位为叶)
监测数据中随机抽取15天的数据作为样本,监测值如茎叶图所示(十位为茎,个位为叶)
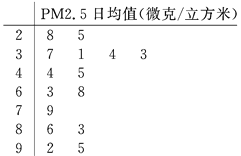
(1)求中位数.
(2)以这15天的![]() 日均值来估计一年的空气质量情况,则一年(按360天计算)中平均有多少天的空气质量达到一级或二级.
日均值来估计一年的空气质量情况,则一年(按360天计算)中平均有多少天的空气质量达到一级或二级.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() 的离心率为
的离心率为![]() ,且过点
,且过点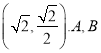 是椭圆的左、右顶点,直线
是椭圆的左、右顶点,直线![]() 过
过![]() 点且与
点且与![]() 轴垂直.
轴垂直.
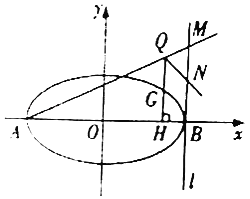
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设![]() 是椭圆
是椭圆![]() 上异于
上异于![]() 的任意一点,作
的任意一点,作![]() 轴于点
轴于点![]() ,延长
,延长![]() 到点
到点![]() 使得
使得![]() ,连接
,连接![]() 并延长交直线
并延长交直线![]() 于
于![]() 点,
点,![]() 点为线段
点为线段![]() 的中点,判断直线
的中点,判断直线![]() 与以
与以![]() 为直径的圆
为直径的圆![]() 的位置关系,并证明你的结论.
的位置关系,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】部分与整体以某种相似的方式呈现称为分形,一个数学意义上分形的生成是基于一个不断迭代的方程式,即一种基于递归的反馈系统.分形几何学不仅让人们感悟到科学与艺木的融合,数学与艺术审美的统一,而且还有其深刻的科学方法论意义.如图,由波兰数学家谢尔宾斯基1915年提出的谢尔宾斯基三角形就属于-种分形,具体作法是取一个实心三角形,沿三角形的三边中点连线,将它分成4个小三角形,去掉中间的那一个小三角形后,对其余3个小三角形重复上述过程逐次得到各个图形.

若在图④中随机选取-点,则此点取自阴影部分的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com