
分析 (1)方法一,分离常数法,在结合基本不等式的性质即可得到答案.方法二:判别式法.
(2)构造已知等式关系,直接利用基本不等式的性质即可得到答案.
解答 解:(1)方法一,分离常数法,
∵x>-1,
∴x+1>0,
那么:$y=\frac{{{x^2}+7x+10}}{x+1}=\frac{{{{(x+1)}^2}+5(x+1)+4}}{x+1}$=(x+1)+$\frac{4}{x+1}+5≥2\sqrt{(x+1)•\frac{4}{x+1}}+5=9$.
当且仅当$x+1=\frac{4}{x+1}$.即x=1时,取等号成立.
∴当x>-1时,y=$\frac{{{x^2}+7x+10}}{x+1}$的最小值为9.
方法二:判别式法.
解:(1)由y=$\frac{{{x^2}+7x+10}}{x+1}$
⇒y(x+1)=x2+7x+10
⇒x2+(7-y)x+10-y=0
方程有解:△≥0,即:(7-y)2-4(10-y)≥0
解得:y≥9或y≤1
又∵x>-1,∴x+1>0,x2+7x+10>0
所以y>0
故当x>-1时,y=$\frac{{{x^2}+7x+10}}{x+1}$的最小值为9.此时x=1.
(2)方法一:构造基本不等式
∵3x+4y=12.要求xy的最大值,xy必须同号.
∴$xy=\frac{1}{12}(3x)•(4y)≤\frac{1}{12}{(\frac{3x+4y}{2})^2}=3$.
当且仅当3x=4y=6.即$x=2,y=\frac{3}{2}$时等号成立.
故:xy取最大值为3.此时$x=2,y=\frac{3}{2}$.
方法二:消元法
∵3x+4y=12.那么:y=3-$\frac{3}{4}x$.
则xy=x(3-$\frac{3}{4}x$)=$-\frac{3}{4}{x}^{2}+3x$
令u=$-\frac{3}{4}{x}^{2}+3x$
由二次函数的性质可得:当x=2时,u取得最大值,即最大值为3.
∵y=3-$\frac{3}{4}x$,
解得:y=$\frac{3}{2}$
故:xy取最大值为3.此时$x=2,y=\frac{3}{2}$.
点评 本题考查了基本不等式性质的灵活应用.属于基础题.


科目:高中数学 来源: 题型:解答题
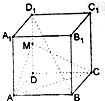 如图,在正方体ABCD-A1B1C1D1中,M为DD1的中点,AB=2.
如图,在正方体ABCD-A1B1C1D1中,M为DD1的中点,AB=2.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com