练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

     已知函数f(x)＝若对任意的x∈R，不等式f(x)≤m2－m恒成立，则实数m的取值范围为________．


    ∪[1，＋∞)


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


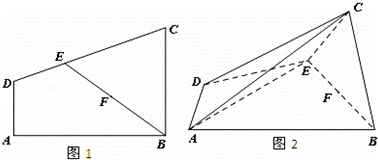
    如图1，在直角梯形ABCD中，AD∥BC，AD⊥AB，AD=1，BC=2，E为CD上一点，且DE=1，EC=2，现沿BE折叠使平面BCE⊥平面ABED，F为BE的中点．图2所示．

    （1）求证：AE⊥平面BCE；

    （2）能否在边AB上找到一点P使平面ACE与平面PCF所成角的余弦值为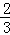？若存在，试确定点P的位置，若不存在请说明理由．

    　

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数f(x)＝log4(ax2＋2x＋3)．

    (1)若f(1)＝1，求f(x)的单调区间；

    (2)是否存在实数a，使f(x)的最小值为0？若存在，求出a的值；若不存在，说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    函数y＝在(－1，＋∞)上单调递增，则a的取值范围是(　　)

    A．a>3  B．a<3

    C．a≤－3  D．a≥－3

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设函数f(x)＝是R上的减函数，则实数a的取值范围为(　　)

    A．(－∞，2)  B.

    C．(0，2)  D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    下列函数中，与函数y＝－3|x|的奇偶性相同的是(　　)

    A．y＝－  B．y＝log2x

    C．y＝－x2  D．y＝x3－1

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数f(x)＝则下列结论正确的是(　　)

    A．f(x)是偶函数

    B．f(x)是增函数

    C．f(x)是周期函数

    D．f(x)的值域为[－1，＋∞)

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图K7­3所示是二次函数y＝ax2＋bx＋c的图像的一部分，图像过点A(－3，0)，对称轴方程为x＝－1.给出下面四个结论：①b2＞4ac；②2a－b＝1；③a－b＋c＝0；④5a＜b.其中正确的结论是(　　)

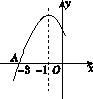
    图K7­3

    A．②④  B．①④

    C．②③  D．①③

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设函数f(x)＝|x＋a|，g(x)＝x－1，对于任意的x∈R，不等式f(x)≥g(x)恒成立，则实数a的取值范围是(　　)

    A．(－∞，－1]  B．(－∞，－1)

    C．(－1，＋∞)  D．[－1，＋∞)

    查看答案和解析>>

    同步练习册答案