
分析 (1)将抛物线转化成标准方程,求的焦点坐标,$|{MN}|=\frac{4}{5}|{FN}|$,根据抛物线的第二定义,即可求得丨MN丨=$\frac{1}{a}$,求得N点坐标,代入抛物线方程即可求得a值,求得抛物线方程;
(2)设出直线l的方程,代入抛物线方程,根据韦达定理即弦长公式求得H点坐标、丨AB丨和丨AH丨,同理设出直线CD:y=-$\frac{1}{k}$x+k2+$\frac{3}{2}$,求得Q点坐标、丨CD丨和丨HQ丨2,在Rt△ACD中,丨AQ丨=$\frac{1}{2}$丨CD丨,根据勾股定理丨AH丨2+丨HQ丨2=丨AQ丨2,即可求得k值,求得直线方程.
解答 解:(1)由已知抛物线C:x2=$\frac{1}{a}$y(a>0)的焦点F(0,$\frac{1}{4a}$),
由$|{MN}|=\frac{4}{5}|{FN}|$,得丨FN丨=$\frac{5}{4}$丨MN丨=丨MN丨+$\frac{1}{4a}$,即丨MN丨=$\frac{1}{a}$,
点N(2,4a),所以$\frac{1}{a}$=4a(a>0)a=$\frac{1}{2}$,
所以抛物线方程:x2=2y;
(2)设AB与CD相交于H,CD的中点为Q,
由题意可知直线m斜率存在且不为0,设A(x1,y1),B(x2,y2),
设直线方程l:y=kx+$\frac{1}{2}$,代入抛物线方程x2=2y,整理得:x2-2kx-1=0,
由韦达定理可知:x1+x2=2k,x1•x2=-1,
H(k,k2+$\frac{1}{2}$),丨AB丨=$\sqrt{(1+{k}^{2})[(2k)^{2}-4×(-1)]}$=2(2+k2),
丨AH丨=2+k2,
∴lCD:y=-$\frac{1}{k}$x+k2+$\frac{3}{2}$,与x2=2y联立得:x2+$\frac{2}{k}$x-(2k2+3)=0,
设C(x3,y3),D(x4,y4),
由韦达定理可知:x1+x2=-$\frac{2}{k}$,x1•x2=-(2k2+3),
求得Q(-$\frac{1}{k}$,$\frac{1}{{k}^{2}}$+k2+$\frac{3}{2}$),=(k+$\frac{1}{k}$)2+($\frac{1}{{k}^{2}}$+1)2,
丨CD丨=$\sqrt{(1+\frac{1}{{k}^{2}})[\frac{4}{{k}^{2}}+4(2{k}^{2}+3)]}$=$\sqrt{\frac{4(1+{k}^{2})^{2}(2{k}^{2}+1)}{{k}^{4}}}$,
在Rt△ACD中,丨AQ丨=$\frac{1}{2}$丨CD丨,又丨AH丨2+丨HQ丨2=丨AQ丨2,
(1+k2)2+(k+$\frac{1}{k}$)2+($\frac{1}{{k}^{2}}$+1)2=$\frac{(1+{k}^{2})(2{k}^{2}+1)}{{k}^{4}}$,
解得k=±1,
直线l的方程为y=±x+$\frac{1}{2}$
点评 本题考查抛物线的标准方程及其简单性质,直线与抛物线的位置关系,考查韦达定理及弦长公式的应用,考查综合分析问题解决问题的能力,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:2016-2017学年内蒙古高二文上月考一数学试卷(解析版) 题型:选择题
已知双曲线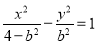
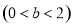 与
与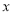 轴交于
轴交于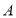 、
、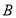 两点,点
两点,点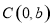 ,则
,则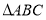 面积的最大值为( )
面积的最大值为( )
A.2 B.4 C.6 D.8
查看答案和解析>>
科目:高中数学 来源:2016-2017学年江西吉安一中高二上段考一数学(理)试卷(解析版) 题型:解答题
已知圆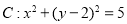 ,直线
,直线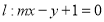 .
.
(1)求证:对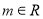 ,直线
,直线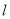 与圆
与圆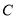 总有两个不同交点;
总有两个不同交点;
(2)若圆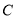 与直线
与直线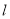 相交于
相交于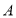 ,
,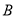 两点,求弦
两点,求弦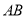 的长度最小值.
的长度最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
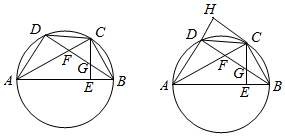 如图,已知D为以AB为斜边的Rt△ABC的外接圆O上一点,CE⊥AB,BD交AC,CE的交点分别为F,G,且G为BF中点,
如图,已知D为以AB为斜边的Rt△ABC的外接圆O上一点,CE⊥AB,BD交AC,CE的交点分别为F,G,且G为BF中点,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
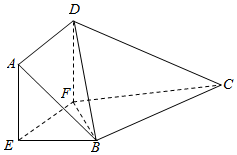 在直角梯形ABCD中,AB∥DC,AD⊥AB,DC=3,AB=2,AD=1,AE=EB,DF=1,现把它沿FE折起,得到如图所示几何体,连接DB,AB,DC,使DC=$\sqrt{5}$,
在直角梯形ABCD中,AB∥DC,AD⊥AB,DC=3,AB=2,AD=1,AE=EB,DF=1,现把它沿FE折起,得到如图所示几何体,连接DB,AB,DC,使DC=$\sqrt{5}$,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com