
如图。在直三棱柱ABC—A1B1C1中,AB=BC=2AA1,∠ABC=90°,M是BC中点。
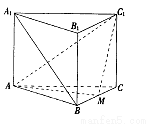
(I)求证:A1B∥平面AMC1;
(II)求直线CC1与平面AMC1所成角的正弦值;
(Ⅲ)试问:在棱A1B1上是否存在点N,使AN与MC1成角60°?若存在,确定点N的位置;若不存在,请说明理由。
(I)由线线平行证得线面平行 (II)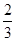 (Ⅲ)
(Ⅲ)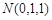 .在棱
.在棱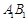 上存在棱
上存在棱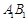 的中点
的中点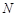 ,使
,使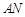 与
与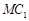 成角
成角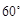 .
.
【解析】
试题分析:(Ⅰ)连接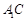 交
交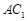 于
于 ,连接
,连接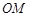 .在三角形
.在三角形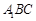 中,
中,
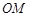 是三角形
是三角形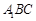 的中位线,
的中位线,
所以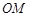 ∥
∥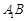 ,
,
又因 平面
平面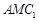 ,
,
所以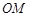 ∥平面
∥平面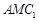 .
.
(Ⅱ)(法一)设直线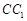 与平面
与平面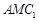 所成角为
所成角为 ,
,
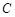 点到平面
点到平面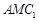 的距离为
的距离为
 ,不妨设
,不妨设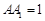 ,则
,则 ,
,
因为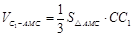 ,
,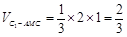 ,
,
所以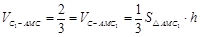 .
.
因为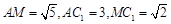 ,
,
所以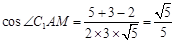 ,
,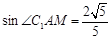 .
.
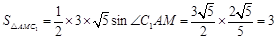 .
.
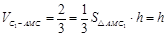 ,
,
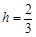 ,
,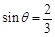 .
.
(法二)如图以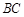 所在的直线为
所在的直线为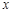 轴, 以
轴, 以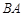 所在的直线为
所在的直线为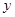 轴, 以
轴, 以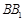 所在的直线为
所在的直线为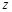 轴,以
轴,以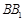 的长度为单位长度建立空间直角坐标系.
的长度为单位长度建立空间直角坐标系.

则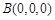 ,
,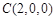 ,
,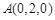 ,
,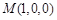 ,
,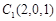 ,
,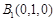 ,
,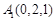 .设直线
.设直线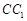 与平面
与平面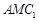 所成角为
所成角为 ,平面
,平面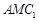 的法向量为
的法向量为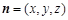 .则有
.则有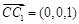 ,
,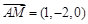 ,
,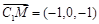 ,
,
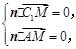
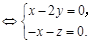 令
令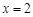 ,得
,得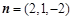 ,
,
设直线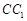 与平面
与平面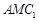 所成角为
所成角为 ,
,
则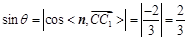 .
.
(Ⅲ)假设直线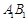 上存在点
上存在点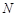 ,使
,使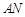 与
与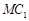 成角为
成角为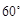 .
.
设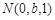 ,则
,则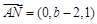 ,
,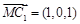 .
.
设其夹角为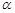 ,
,
所以,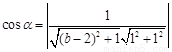
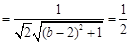 ,
,
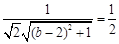 ,
,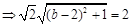
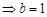 或
或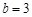 (舍去),
(舍去),
故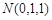 .所以在棱
.所以在棱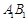 上存在棱
上存在棱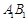 的中点
的中点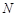 ,使
,使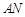 与
与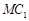 成角
成角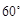 .
.
考点:直线与平面平行的判定;直线与平面垂直的判定;直线与平面所成的角.
点评:此题考查直线与平面平行的判断及直线与平面垂直的判断,第一问此类问题一般先证明两个面平行,再证直线和面平行,这种做题思想要记住,此类立体几何题是每年高考必考的一道大题,难度比较大,计算要仔细.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
如图,在直三棱柱AB-A1B1C1中.∠ BAC=90°,AB=AC=AA1 =1.D是棱CC1上的一P是AD的延长线与A1C1的延长线的交点,且PB1∥平面BDA.
(I)求证:CD=C1D:
(II)求二面角A-A1D-B的平面角的余弦值;
(Ⅲ)求点C到平面B1DP的距离.

查看答案和解析>>
科目:高中数学 来源:2011年四川省招生统一考试理科数学 题型:解答题
(本小题共l2分)
如图,在直三棱柱AB-A1B1C1中.∠ BAC=90°,AB=AC=AA1 =1.D是棱CC1上的一[来源:]
P是AD的延长线与A1C1的延长线的交点,且PB1∥平面BDA.
(I)求证:CD=C1D:
(II)求二面角A-A1D-B的平面角的余弦值;
(Ⅲ)求点C到平面B1DP的距离.

查看答案和解析>>
科目:高中数学 来源:2011年高考试题数学理(四川卷)解析版 题型:解答题
(本小题共l2分)
如图,在直三棱柱AB-A1B1C1中.∠ BAC=90°,AB=AC=AA1 =1.D是棱CC1上的一
P是AD的延长线与A1C1的延长线的交点,且PB1∥平面BDA.
(I)求证:CD=C1D:
(II)求二面角A-A1D-B的平面角的余弦值;
(Ⅲ)求点C到平面B1DP的距离.

查看答案和解析>>
科目:高中数学 来源:四川省高考真题 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:
如图,在直三棱柱AB-A1B1C1中.∠ BAC=90°,AB=AC=AA1 =1.D是棱CC1上的一点,P是AD的延长线与A1C1的延长线的交点,且PB1∥平面BDA.
(I)求证:CD=C1D:
(II)求二面角A-A1D-B的平面角的余弦值;
(Ⅲ)求点C到平面B1DP的距离.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com