已知复数z满足：z2+z+1=0，则1+z+z2+z3+…+z2007= ．
【答案】
分析：先把z求出来，再找到z的特性，然后把问题分组，构造z
2+z+1，利用z
2+z+1=0和z的特性即可求值
解答：解：∵复数z满足z
2+z+1=0
∴
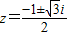
∴z
3=1
又1+z+z
2+z
3+…+z
2007=（1+z+z
2）+（z
3+z
4+z
5）+（z
6+z
7+z
8）+…+（z
2004+z
2005+z
2006）+z
2007
=（1+z+z
2）+z
3（1+z+z
2）+z
6（1+z+z
2）+…+z
2004（1+z+z
2）+z
2007=z
2007=（z
3）
669=1
点评：本题考查复数运算，要注意问题的变形和条件的灵活应用．属简单题
一线名师提优试卷系列答案
阳光试卷单元测试卷系列答案
