【答案】
分析:(Ⅰ)把a=1代入函数解析式,然后取特殊值x=-1,求得对应点的纵坐标大于b,说明函数f(x)的图象不能总在直线y=b的下方;
(Ⅱ)求出原函数的导函数,解出导函数的零点,然后对a进行分类讨论,找出能使函数f(x)在(0,2)上是增函数a的取值范围.或是求出导函数后,利用分离变量法把a分离出来,把导函数恒大于等于0转化为a恒大于等于一个函数的最大值问题;
(Ⅲ)因为方程f(x)=-x
3+ax
2+b=0最多只有3个根,由方程f(x)=0在(-1,0)和(0,1)内各有一个根列式f(-1)•f(0)=b(1+a+b)<0与f(0)•f(1)=b(-1+a+b)<0,然后分b>0,b<0和b=0讨论即可得到a的取值范围.
解答:(Ⅰ)解:当a=1时,f(x)=-x
3+x
2+b,
因为f(-1)=b+2>b,
所以,函数f(x)的图象不能总在直线y=b的下方.
(Ⅱ)解:法一、
由f(x)=-x
3+ax
2+b,得f
′(x)=-3x
2+2ax,
令f
′(x)=-3x
2+2ax=0,解得x=0或
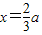
,
①当a<0时,由f
′(x)>0,解得
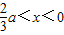
,
所以f(x)在

上是增函数,与题意不符,舍去;
②当a=0时,由f
′(x)=-3x
2≤0,
所以f(x)在R上是减函数,与题意不符,舍去;
③当a>0时,由f
′(x)>0,解得0<x<
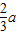
,
所以f(x)在
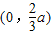
上是增函数,
又f(x)在(0,2)上是增函数,所以
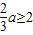
,解得a≥3,
综上,a的取值范围为[3,+∞).
法二、
由f(x)=-x
3+ax
2+b,得f
′(x)=-3x
2+2ax,
要使函数f(x)在(0,2)上是增函数,
则需f
′(x)=-3x
2+2ax≥0对任意x∈(0,2)恒成立,
即2ax≥3x
2对任意x∈(0,2)恒成立,
也就是a
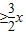
对任意x∈(0,2)恒成立,
因为y=
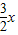
在x∈(0,2)上为增函数,所以a
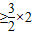
=3.
所以,a的取值范围为[3,+∞).
(Ⅲ)证明:因为方程f(x)=-x
3+ax
2+b=0最多只有3个根,
由题意,方程在区间(-1,0)内仅有一根,
所以f(-1)•f(0)=b(1+a+b)<0,
方程在区间(0,1)内仅有一根,
所以f(0)•f(1)=b(-1+a+b)<0,
当b>0时,由b(1+a+b)<0得,1+a+b<0,即a<-b-1,
由b(-1+a+b)<0得,-1+a+b<0,即a<-b+1,
因为-b-1<-b+1,所以a<-b-1<-1,即a<-1;
当b<0时,由b(1+a+b)<0得,1+a+b<0,即a>-b-1,
由b(-1+a+b)<0得,-1+a+b<0,即a>-b+1,
因为-b-1<-b+1,所以a>-b+1>1,即a>1;
当b=0时,因为f(0)=0,所以f(x)=0有一根0,
这与题意不符.
∴a>1或a<-1.
点评:本题考查了利用函数的导函数研究函数的单调性,考查了分类讨论得数学思想,训练了利用分离变量求函数的最值,考查了根的存在性及根的个数的判断,在区间(a,b)内,若f(a)•f(b)<0,函数在区间(a,b)内必有根.此题是中档题.

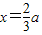 ,
,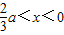 ,
, 上是增函数,与题意不符,舍去;
上是增函数,与题意不符,舍去;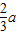 ,
,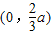 上是增函数,
上是增函数,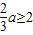 ,解得a≥3,
,解得a≥3,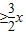 对任意x∈(0,2)恒成立,
对任意x∈(0,2)恒成立,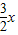 在x∈(0,2)上为增函数,所以a
在x∈(0,2)上为增函数,所以a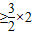 =3.
=3.

 阅读快车系列答案
阅读快车系列答案