
���� ��1��������ɵã�a+x��2=k��a-x��2����Ϊ��1-k��x2+2a��1+k��x+��1-k��a2=0��x��R������
����������$\left\{\begin{array}{l}{1-k=0}\\{2a��1+k��=0}\\{��1-k��{a}^{2}=0}\end{array}\right.$���ⷽ�̼����жϣ�
��2��Ӵ����ɵ�sin��a+x��=ksin��a-x�����������ǺͲʽ�����������Һ�����ֵ�ɵõ��������ԣ�
��3���ɣ�1��1���ͣ�2��-1�����Ǻ���f��x���ġ��������ԡ�������f��1+x��=f��1-x����f��2+x��=-f��2-x�����ɵ�f��x��Ϊ����Ϊ4�ĺ��������0��x��1��1��x��2��2��x��3��3��x��4��x=0��1��2��3��4�ĺ�������ʽ���ɵ�2014��x��2015��2015��x��2016��x=2014��2015��2016�Ľ���ʽ�����ɵõ�������㣮
��� �⣺��1����f��x��=x2��f��a+x��=kf��a-x�����ɵ�
��a+x��2=k��a-x��2������1-k��x2+2a��1+k��x+��1-k��a2=0��x��R������
����������$\left\{\begin{array}{l}{1-k=0}\\{2a��1+k��=0}\\{��1-k��{a}^{2}=0}\end{array}\right.$�����$\left\{\begin{array}{l}{a=0}\\{k=1}\end{array}\right.$����k=1��0��a���ڣ�
����f��x��=x2��M��
��2����f��x��=sinx��M�ã�sin��a+x��=ksin��a-x����
sinacosx+cosasinx=k��sinacosx-cosasinx����
���ԣ�1+k��cosasinx+��1-k��sinacosx=0��
$\sqrt{{k}^{2}+2kcos2a+1}$sin��x+�գ�=0�������x��R��������ֻ��k2+2kcos2a+1=0��
��cos2a=-$\frac{1}{2}$��k+$\frac{1}{k}$��������|k+$\frac{1}{k}$|��2�����ҽ���k=��1ʱ���Ⱥų�������
����|cos2a|��1������Ϊ|cos2a|��1����|cos2a|=1��
����k=1ʱ��cos2a=-1��a=n��+$\frac{��}{2}$��n��Z��
k=-1ʱ��cos2a=1��a=n�У�n��Z��
�ʺ���f��x���ġ��������ԡ�Ϊ��n��+$\frac{��}{2}$��1���ͣ�n�У�-1����n��Z��
��3����Ϊ��1��1���ͣ�2��-1�����Ǻ���f��x���ġ��������ԡ���
����f��1+x��=f��1-x����f��2+x��=-f��2-x��������f��x+4��=f��x����
�ʺ���f��x������4Ϊ���ڵĺ�����
��0��x��1����1��2-x��2����ʱf��x��=f��2-x��=-cos��$\frac{��}{2}$x����
��2��x��3����1��4-x��2����ʱf��x��=-f��4-x��=-cos��$\frac{��}{2}$x����
��3��x��4����0��4-x��1����ʱf��x��=-f��4-x��=cos��$\frac{��}{2}$x����
f��x��=$\left\{\begin{array}{l}{-cos��\frac{��}{2}x����0��x��1}\\{cos��\frac{��}{2}x����1��x��2}\\{-cos��\frac{��}{2}x����2��x��3}\\{cos��\frac{��}{2}x����3��x��4}\\{0��x=0��1��2��3��4}\end{array}\right.$��f��x��=$\left\{\begin{array}{l}{-cos��\frac{��}{2}x����2014��x��2015}\\{cos��\frac{��}{2}x����2015��x��2016}\\{0��x=2014��2015��2016}\end{array}\right.$
��2014��x��2016ʱ������f��x�������ֱ�Ϊ2014��2015��2016��
���� ���⿼���¶������������ã����麯�������ʺ����ã���Ҫ���麯���������Ժͺ����Ľ���ʽ�����������������������������������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
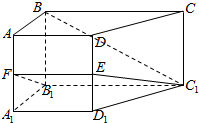 ��ͼ��ʾ���ڲ��ⴹֱ�ڵ����������ABCD-A1B1C1D1�У�AD��BC��AD��AB��AB=$\sqrt{2}$��AD=2��BC=4��AA1=2��E��F�ֱ���DD1��AA1���е㣮
��ͼ��ʾ���ڲ��ⴹֱ�ڵ����������ABCD-A1B1C1D1�У�AD��BC��AD��AB��AB=$\sqrt{2}$��AD=2��BC=4��AA1=2��E��F�ֱ���DD1��AA1���е㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
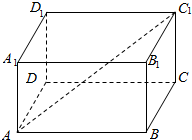 ��ͼ���ڳ�����ABCD-A1B1C1D1�У���֪A1A=1��AD=1��AB=$\sqrt{2}$������Խ���AC1��ƽ��ABCD���ɽǵĴ�СΪ30�㣮
��ͼ���ڳ�����ABCD-A1B1C1D1�У���֪A1A=1��AD=1��AB=$\sqrt{2}$������Խ���AC1��ƽ��ABCD���ɽǵĴ�СΪ30�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
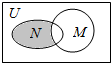
| A�� | {2��3} | B�� | {0��1��2} | C�� | {1��2��3} | D�� | {0��1} |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
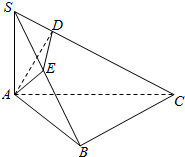 ��ͼ��������S-ABC�У���ABC=90�㣬SA��ƽ��ABC����A��SB��SC�ϵ���Ӱ�ֱ�ΪE��D��
��ͼ��������S-ABC�У���ABC=90�㣬SA��ƽ��ABC����A��SB��SC�ϵ���Ӱ�ֱ�ΪE��D���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com