
 )β(α,β,x∈R+),
)β(α,β,x∈R+),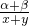 )α+β≤(
)α+β≤(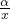 )α•(
)α•(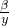 )β;
)β;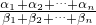 )α1+α2+…+αn≤(
)α1+α2+…+αn≤(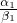 )α1•(
)α1•(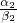 )α2…(
)α2…(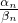 )αn.
)αn. )β+(1+x)α•β(1+
)β+(1+x)α•β(1+ )β-1•(-1)•
)β-1•(-1)• =
= ,
, ,∞)时f′(x)>0,x∈(0,
,∞)时f′(x)>0,x∈(0, )时,f′(x)<0.
)时,f′(x)<0. )=(
)=(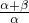 )α(
)α(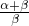 )β.
)β. )≤f(
)≤f( ),∴(
),∴(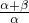 )α•(
)α•(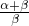 )β≤(
)β≤( )α•(
)α•(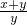 )β,
)β,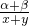 )α+β≤(
)α+β≤(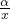 )α•(
)α•(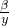 )β.
)β.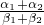 )α1+α2≤(
)α1+α2≤(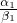 )α1•(
)α1•(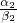 )α2,
)α2,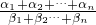 )α1+α2+…+αn≤(
)α1+α2+…+αn≤(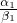 )α1•(
)α1•(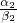 )α2…(
)α2…(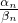 )αn,
)αn,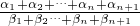 )α1+α2+…+αn+αn+1
)α1+α2+…+αn+αn+1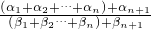 ](α1+α2+…+αn)+αn+1
](α1+α2+…+αn)+αn+1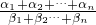 )α1+α2+…+αn•(
)α1+α2+…+αn•(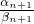 )αn+1
)αn+1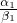 )α1•(
)α1•(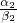 )α2…(
)α2…(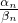 )αn•(
)αn•(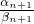 )αn+1.
)αn+1. ,从而可知x∈(
,从而可知x∈( ,+∞)时f′(x)>0,x∈(0,
,+∞)时f′(x)>0,x∈(0, )时,f′(x)<0.故可求f(x)的最小值;
)时,f′(x)<0.故可求f(x)的最小值; )≤f(
)≤f( ),可得(
),可得(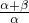 )α•(
)α•(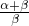 )β≤(
)β≤( )α•(
)α•(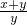 )β,从而得证;
)β,从而得证;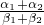 )α1+α2≤(
)α1+α2≤(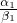 )α1•(
)α1•(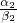 )α2,假设n=k时,成立,即(
)α2,假设n=k时,成立,即(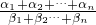 )α1+α2+…+αn≤(
)α1+α2+…+αn≤(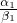 )α1•(
)α1•(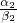 )α2…(
)α2…(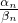 )αn,再证明当n=k+1时也,成立.
)αn,再证明当n=k+1时也,成立.

 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案科目:高中数学 来源: 题型:
| x | 1+ax |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com