
分析 设A(x1,y1),B(x2,y2).直线方程与椭圆方程联立化为:(3+4k2)x2+8kbx+4b2-12=0,△>0,由AB被y轴平分,可得x1+x2=0,因此kb=0.k=0或b=0.由PA⊥PB,可得$\overrightarrow{PA}•\overrightarrow{PB}$=(x1-1)(x2-1)+$({y}_{1}-\frac{3}{2})({y}_{2}-\frac{3}{2})$=(x1-1)(x2-1)+$(k{x}_{1}+b-\frac{3}{2})$$(k{x}_{2}+b-\frac{3}{2})$.对k=0与b=0分类讨论利用根与系数的关系即可得出.
解答 解:设A(x1,y1),B(x2,y2).
联立$\left\{\begin{array}{l}{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1}\\{y=kx+b}\end{array}\right.$,化为:(3+4k2)x2+8kbx+4b2-12=0,
△>0,∴64k2b2-4(3+4k2)(4b2-12)>0,(*).
∴x1+x2=$\frac{-8kb}{3+4{k}^{2}}$,x1•x2=$\frac{4{b}^{2}-12}{3+4{k}^{2}}$,
∵AB被y轴平分,∴x1+x2=0,∴kb=0.
∴k=0或b=0.
∵PA⊥PB,
∴$\overrightarrow{PA}•\overrightarrow{PB}$=(x1-1)(x2-1)+$({y}_{1}-\frac{3}{2})({y}_{2}-\frac{3}{2})$=(x1-1)(x2-1)+$(k{x}_{1}+b-\frac{3}{2})$$(k{x}_{2}+b-\frac{3}{2})$.
①若k=0,则$\overrightarrow{PA}•\overrightarrow{PB}$=(x1-1)(x2-1)+$(b-\frac{3}{2})^{2}$=0,
∴x1x2-(x1+x2)+1+$(b-\frac{3}{2})^{2}$=0,
∴$\frac{1}{3}(4{b}^{2}-12)$+0+1+$(b-\frac{3}{2})^{2}$=0,化为20b2-12b-27=0,解得b=$\frac{3±3\sqrt{46}}{10}$,不满足△>0,舍去.
②若b=0,则$\overrightarrow{PA}•\overrightarrow{PB}$=(x1-1)(x2-1)+$(k{x}_{1}-\frac{3}{2})(k{x}_{2}-\frac{3}{2})$=0,
∴(1+k2)x1x2-$(\frac{3k}{2}+1)$(x1+x2)+$\frac{13}{4}$=0,
∴(1+k2)$\frac{-12}{3+4{k}^{2}}$+$\frac{13}{4}$=0,解得k=$±\frac{3}{2}$,满足△>0.此时直线l的方程为:y=$±\frac{3}{2}$x.
综上可得:直线l的方程为y=$±\frac{3}{2}$x.
故答案为:y=$±\frac{3}{2}$x.
点评 本题考查了椭圆的标准方程及其性质、直线与椭圆相交问题、一元二次方程的根与系数的关系、数量积运算性质,考查了分类讨论方法、推理能力与计算能力,属于难题.


 名师指导一卷通系列答案
名师指导一卷通系列答案科目:高中数学 来源: 题型:解答题
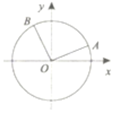 如图,在平面直角坐标系xOy中,以O为角的顶点,x轴正半轴为始边的角α、β的终边分别与单位圆交于点A,B,若点A的横坐标是$\frac{4}{5}$,点B的纵坐标是$\frac{\sqrt{3}}{2}$.
如图,在平面直角坐标系xOy中,以O为角的顶点,x轴正半轴为始边的角α、β的终边分别与单位圆交于点A,B,若点A的横坐标是$\frac{4}{5}$,点B的纵坐标是$\frac{\sqrt{3}}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | m=10 n=20 n=m m=n | |
| B. | m=10 n=20 s=m n=s | |
| C. | m=10 n=20 s=m m=n n=s | |
| D. | m=10 n=20 s=m t=n n=s m=n |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
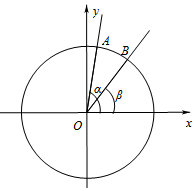 如图,在平面直角坐标系xOy中,以O为顶点,x轴的非负半轴为始边作两个锐角α,β,它们的终边分别与单位圆交于A,B两点.已知A,B的横坐标分别为$\frac{\sqrt{2}}{10},\frac{3}{5}$.
如图,在平面直角坐标系xOy中,以O为顶点,x轴的非负半轴为始边作两个锐角α,β,它们的终边分别与单位圆交于A,B两点.已知A,B的横坐标分别为$\frac{\sqrt{2}}{10},\frac{3}{5}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com