
分析 (Ⅰ)利用数列的通项公式与数列和的关系式,化简已知条件,推出数列是等差数列,然后求数列{an}的通项公式.
(Ⅱ)化简${b_n}=\frac{3}{{{a_{2n}}{a_{2n+2}}}}$,利用裂项消项法求解数列的和即可.
解答 解:(Ⅰ)由${a_n}^2-2{S_n}=2-{a_n}$得${a_{n+1}}^2-2{S_{n+1}}=2-{a_{n+1}}$
相减得${a_{n+1}}^2-{a_n}^2-2({{S_{n+1}}-{S_n}})={a_n}-{a_{n+1}}$
即${a_{n+1}}^2-{a_n}^2-({{a_{n+1}}+{a_n}})=0$,(an+1-an)(an+1+an)-(an+1+an)=0
因为an>0 解得an+1-an=1(n∈N*)
故数列{an}为等差数列,且公差d=1 …(4分)
又a12-2S1=2-a1
解得a1=2或a1=-1(舍去)
an=n+1 …(6分)
$(Ⅱ){b}_{n}=\frac{3}{{a}_{2n}{a}_{2n+2}}=\frac{3}{(2n+1)(2n+3)}=\frac{3}{2}(\frac{1}{2n+1}-\frac{1}{2n+3})$,
$则{T_n}=\frac{3}{2}[{({\frac{1}{3}-\frac{1}{5}})+({\frac{1}{5}-\frac{1}{7}})+…+({\frac{1}{2n+1}-\frac{1}{2n+3}})}]$…(10分)
=$\frac{3}{2}({\frac{1}{3}-\frac{1}{2n+3}})=\frac{n}{2n+3}$…(12分)
点评 本题考查数列的递推关系式的应用,数列求和的方法,考查转化思想以及计算能力.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 等腰三角形 | B. | 直角三角形 | C. | 等边三角形 | D. | 不确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
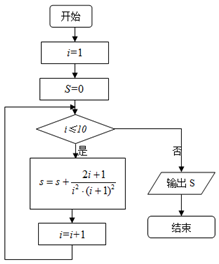
| A. | $\frac{1}{100}$ | B. | $\frac{1}{121}$ | C. | $\frac{99}{100}$ | D. | $\frac{120}{121}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 一个多面体的三视图和直观图如图所示,其中M,N,P分别是AB,SC,SD的中点.
一个多面体的三视图和直观图如图所示,其中M,N,P分别是AB,SC,SD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com