
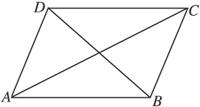
思路分析:本题要求线段长度问题,可以转化为求向量的模来解决.
解:设![]() =a,
=a,![]() =b,则
=b,则![]() =a-b,
=a-b, ![]() =a+b.
=a+b.
而|![]() |=|a-b|=
|=|a-b|=![]() ,
,
∴|![]() |2=5-2a·b=4.①
|2=5-2a·b=4.①
又|![]() |2=|a+b|2=a2+2a·b+b2=|a|2+2a·b+|b|2=1+4+2a·b.
|2=|a+b|2=a2+2a·b+b2=|a|2+2a·b+|b|2=1+4+2a·b.
由①得2a·b=1,
∴|![]() |2=6,∴|
|2=6,∴|![]() |=
|=![]() ,即AC=
,即AC=![]() .
.
温馨提示
(1)合理地选择基底是解决好问题的第一步,虽说任意两个不共线的向量都可以做基底,但选择恰当与否直接关系到解题过程的简单与复杂.
(2)几何问题用向量法解决体现出了较强的优势,有关线段的长度、平行、夹角等问题都可考虑向量法.
(3)在解决本题中,不用解斜三角形,而用向量的数量积及模的知识解决,过程中采取整体代入,使问题解决简捷明快.


科目:高中数学 来源: 题型:
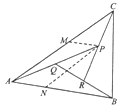
 如图,在△ABC中,设
如图,在△ABC中,设| AB |
| AC |
| AP |
| S平行四边形ANPM |
| S△ABC |
查看答案和解析>>
科目:高中数学 来源: 题型:
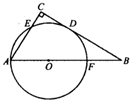 (2012•大连二模)任选一题作答选修:几何证明选讲如图,在△ABC中,∠C=90°,以AB上一点O为圆心,OA长为半径的圆与BC相切于点D,分别交AC、AB于点E、F.
(2012•大连二模)任选一题作答选修:几何证明选讲如图,在△ABC中,∠C=90°,以AB上一点O为圆心,OA长为半径的圆与BC相切于点D,分别交AC、AB于点E、F.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| AB |
| AC |
| AP |
| S平行四边形ANPM |
| S△ABC |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年山东省聊城市某重点高中高三(上)第二次调研数学试卷(理科)(解析版) 题型:解答题
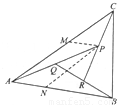
 ,
, ,AP的中点为Q,BQ的中点为R,CR的中点恰为P.
,AP的中点为Q,BQ的中点为R,CR的中点恰为P.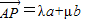 ,求λ和μ的值;
,求λ和μ的值; .
.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年山东省聊城市某重点高中高三(上)第二次调研数学试卷(理科)(解析版) 题型:解答题
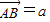 ,
,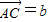 ,AP的中点为Q,BQ的中点为R,CR的中点恰为P.
,AP的中点为Q,BQ的中点为R,CR的中点恰为P.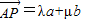 ,求λ和μ的值;
,求λ和μ的值; .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com