
如图,在长方体![]() 中,
中,![]() 点
点![]() 在线段
在线段![]() 上.
上.
(Ⅰ)求异面直线![]() 与
与![]() 所成的角;
所成的角;
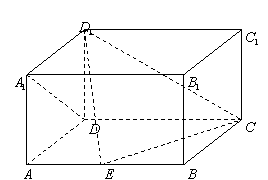 (Ⅱ)若二面角
(Ⅱ)若二面角![]() 的大小为
的大小为![]() ,求点
,求点![]() 到平面
到平面![]() 的距离.
的距离.
解析:本题涉及立体几何线面关系的有关知识, 本题实质上求角度和距离,在求此类问题中,要将这些量归结到三角形中,最好是直角三角形,这样有利于问题的解决,此外用向量也是一种比较好的方法.
答案:解法一:(Ⅰ)连结![]() 。由已知,
。由已知,![]() 是正方形,有
是正方形,有![]() 。
。
∵![]() 平面
平面![]() ,∴
,∴![]() 是
是![]() 在平面
在平面![]() 内的射影。
内的射影。
根据三垂线定理,![]() 得,则异面直线
得,则异面直线![]() 与
与![]() 所成的角为
所成的角为![]() 。
。
作![]() ,垂足为
,垂足为![]() ,连结
,连结![]() ,则
,则![]()
所以![]() 为二面角
为二面角![]() 的平面角,
的平面角,![]() .
.
于是![]()
易得![]() ,所以
,所以![]() ,又
,又![]() ,所以
,所以![]() 。
。
设点![]() 到平面
到平面![]() 的距离为
的距离为![]() .
.
∵![]() 即
即![]() ,
,
∴![]() ,即
,即![]() ,∴
,∴![]() .
.
故点![]() 到平面
到平面![]() 的距离为
的距离为![]() 。
。
解法二:分别以![]() 为
为![]() 轴、
轴、![]() 轴、
轴、![]() 轴,建立空间直角坐标系.
轴,建立空间直角坐标系.
(Ⅰ)由![]() ,得
,得![]()
设![]() ,又
,又![]() ,则
,则![]() 。
。
∵![]() ∴
∴![]()
则异面直线![]() 与
与![]() 所成的角为
所成的角为![]() 。
。
(Ⅱ)![]() 为面
为面![]() 的法向量,设
的法向量,设![]() 为面
为面![]() 的法向量,则
的法向量,则
![]()
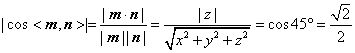
∴![]() . ①
. ①
由![]() ,得
,得![]() ,则
,则![]() ,即
,即![]()
∴![]() ②
②
由①、②,可取![]()
又![]() ,所以点
,所以点![]() 到平面
到平面![]() 的距离
的距离
![]() 。
。


科目:高中数学 来源: 题型:
如图,在长方体![]() 中,点
中,点![]() 分别在
分别在![]() 上,且
上,且![]() ,
,![]() .
.
(1)求证:![]() 平面
平面![]() ;
;
(2)若规定两个平面所成的角是这两个平面所组成的二面角中的锐角(或直角),则在空间有定理:若两条直线分别垂直于两个平面,则这两条直线所成的角与这两个平面所成角相等,试根据上述定理,在![]() 时,求平面
时,求平面![]() 与平面
与平面![]() 所成角的大小.
所成角的大小.

查看答案和解析>>
科目:高中数学 来源:2010-2011学年湖南省高三第一次质检文科数学卷 题型:解答题
(12分)如图,在长方体 中,点
中,点 在棱
在棱 的延长线上,且
的延长线上,且 .
.
(Ⅰ)求证: //平面
//平面 ;
;
(Ⅱ)求证:平面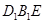
 平面
平面 ;
;

查看答案和解析>>
科目:高中数学 来源:福建省2010届高三高考模拟试卷文科数学 题型:解答题
(本小题12分)如图,在长方体 中,点
中,点 在棱
在棱 的延长线上,且
的延长线上,且 .
.
(1)求证: ∥平面
∥平面 ;
;
(2)求证:平面
 平面
平面 ;
;
(3)求四面体 的体积.
的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com