Question

9．若曲线y=1+$\sqrt{4-{x}^{2}}$与直线kx-y-2k+4=0有两个公共点，则实数k的取值范围是$\frac{5}{12}$＜k≤$\frac{3}{4}$．

Answer 1

分析 先将曲线进行化简得到一个圆心是（0，1）的上半圆，直线y=k（x-2）+4表示过定点（2，4）的直线，利用直线与圆的位置关系可以求实数k的取值范围．

解答 解：因为y=1+$\sqrt{4-{x}^{2}}$，所以x²+（y-1）²=4，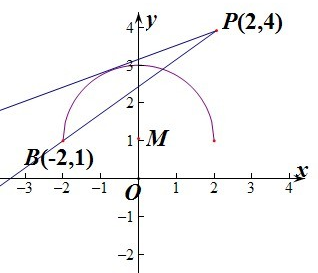
此时表示为圆心M（0，1），半径r=2的圆．
因为x∈[-2，2]，y=1+$\sqrt{4-{x}^{2}}$≥1，
所以表示为圆的上部分．
直线y=k（x-2）+4表示过定点P（2，4）的直线，
当直线与圆相切时，有圆心到直线kx-y+4-2k=0的距离d=$\frac{|3-2k|}{\sqrt{{k}^{2}+1}}$=2，解得k=$\frac{5}{12}$．
当直线经过点B（-2，1）时，直线PB的斜率为k=$\frac{3}{4}$．
所以要使直线与曲线有两个不同的公共点，则必有$\frac{5}{12}$＜k≤$\frac{3}{4}$．
即实数k的取值范围是$\frac{5}{12}$＜k≤$\frac{3}{4}$．
故答案为$\frac{5}{12}$＜k≤$\frac{3}{4}$．

点评 本题主要考查了直线与圆的位置关系的应用以及直线的斜率和距离公式．利用数形结合思想是解决本题的关键．同时要注意曲线化简之后是个半圆，而不是整圆，这点要注意，防止出错．