
| | 患病 | 未患病 | 总计 |
| 服用药 | 15 | 40 | 55 |
| 没服用药 | 20 | 25 | 45 |
| 总计 | 35 | 65 | 100 |
| A.0.025 | B.0.10 | C.0.01 | D.0.005 |
 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:高中数学 来源:不详 题型:解答题
 50名学生在一模数学考试中,成绩都属于区间[60,110]。将成绩按如下方式分成五组:第一组[60,70);第二组[70,80);第三组[80,90);第四组[90,100);第五组[100,110]。部分频率分布直方图如图3所示,及格(成绩不小于90分)的人数为20。
50名学生在一模数学考试中,成绩都属于区间[60,110]。将成绩按如下方式分成五组:第一组[60,70);第二组[70,80);第三组[80,90);第四组[90,100);第五组[100,110]。部分频率分布直方图如图3所示,及格(成绩不小于90分)的人数为20。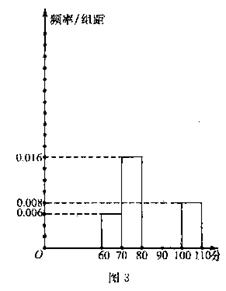
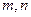 ,求
,求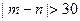 的概率;
的概率;查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,乙队中3人答对的概率分别为
,乙队中3人答对的概率分别为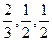 ,且各人答题正确与否相互之间没有影响.用
,且各人答题正确与否相互之间没有影响.用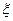 表示甲队的总得分.
表示甲队的总得分.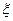 的分布列和数学期望;
的分布列和数学期望;  表示“甲、乙两个队总得分之和等于3”这一事件,用
表示“甲、乙两个队总得分之和等于3”这一事件,用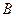 表示“甲队总得分大于乙队总得分”这一事件,求
表示“甲队总得分大于乙队总得分”这一事件,求 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 过第二
过第二 次烧制后,甲、乙、丙三件产品合格的概率依次为0.6,0.5,0.75。
次烧制后,甲、乙、丙三件产品合格的概率依次为0.6,0.5,0.75。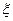 ,求随机变量
,求随机变量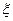 的期望。
的期望。查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| | 存活数 | 死亡数 | 合计 |
| 新措施 | 132 | 18 | 150 |
| 对照 | 114 | 36 | 150 |
| 合计 | 246 | 54 | 300 |
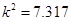 ,故我们由此认为 “新措施对防治非典有效” 的把握为( )
,故我们由此认为 “新措施对防治非典有效” 的把握为( )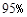 C.
C.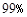 D.
D.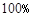
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 进入下一轮考核,否则被淘汰,已知某选手能正确回答第一、二、三、四轮问题的概率分别为
进入下一轮考核,否则被淘汰,已知某选手能正确回答第一、二、三、四轮问题的概率分别为 、
、 、
、 、
、 ,且各
,且各 轮问题能否正确回答互不影响。
轮问题能否正确回答互不影响。 个数记为
个数记为 ,求随机变量
,求随机变量 的分布列和期望。
的分布列和期望。查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com