
【题目】在矩形![]() 中,
中, ![]() ,
, ![]() 是边
是边![]() 的中点,如图(1),将
的中点,如图(1),将![]() 沿直线
沿直线![]() 翻折到
翻折到![]() 的位置,使
的位置,使![]() ,如图(2).
,如图(2).
(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)已知![]() ,
, ![]() ,
, ![]() 分别是线段
分别是线段![]() ,
, ![]() ,
, ![]() 上的点,且
上的点,且![]() ,
, ![]() ,
, ![]() 平面
平面![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.


【答案】(1)见解析;(2) 直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.
【解析】试题分析:(Ⅰ)先证明![]() 平面
平面![]() ,从而可得
,从而可得![]() ,由平面几何知识可得
,由平面几何知识可得![]() ,由线面垂直的判定定理可得BE⊥平面PCE,进而由面面垂直的判定定理可得结论;(Ⅱ)以点
,由线面垂直的判定定理可得BE⊥平面PCE,进而由面面垂直的判定定理可得结论;(Ⅱ)以点![]() 为原点,分别以
为原点,分别以![]() ,
, ![]() 所在直线为
所在直线为![]() ,
, ![]() 轴,以经过点
轴,以经过点![]() 且垂直于平面
且垂直于平面![]() 的直线为
的直线为![]() 轴建立空间直角坐标系,求出平面
轴建立空间直角坐标系,求出平面![]() 的法向量以及直线的方向向量,利用空间向量夹角余弦公式可得结果.
的法向量以及直线的方向向量,利用空间向量夹角余弦公式可得结果.
试题解析:(Ⅰ)证明:连结![]() ,由题意可知
,由题意可知![]() .
.
又因为![]() ,
, ![]() ,
, ![]() ,
, ![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
又因为![]() 平面
平面![]() ,
,
所以![]() .
.
又因为在矩形![]() 中,
中, ![]() ,
,
所以![]() .
.
又因为![]() ,
, ![]() ,
, ![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
又因为![]() 平面
平面![]() ,
,
所以平面![]() 平面
平面![]() .
.


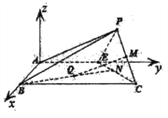
(Ⅱ)在图(2)中,以点![]() 为原点,分别以
为原点,分别以![]() ,
, ![]() 所在直线为
所在直线为![]() ,
, ![]() 轴,以经过点
轴,以经过点![]() 且垂直于平面
且垂直于平面![]() 的直线为
的直线为![]() 轴建立空间直角坐标系,如下图所示.
轴建立空间直角坐标系,如下图所示.
由题意可知, ![]() ,
, ![]() ,
, ![]()
取![]() 的中点
的中点![]() ,连结
,连结![]() .
.
由(Ⅰ)可知平面![]() 平面
平面![]() .
.
又因为![]() ,所以
,所以![]() .
.
又因为平面![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
可得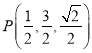 .
.
又因为![]() ,所以
,所以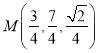 .
.
因为![]() ,可得
,可得![]() .
.
设![]() ,可得
,可得![]() .
.
所以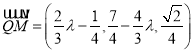 .
.
又因为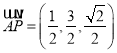 ,
, ![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,
,
则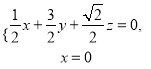 令
令![]() ,可得
,可得![]() ,
,
所以![]()
因为![]() 平面
平面![]() ,所以
,所以![]() ,可得
,可得![]() .
.
所以 .
.
由(Ⅰ)可知![]() 平面
平面![]() ,所以
,所以![]() 是平面
是平面![]() 的一个法向量,
的一个法向量, ![]() .
.
可得![]() .
.
所以直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.
【方法点晴】本题主要考查面面垂直的判定定理、利用空间向量求线面角,属于难题.空间向量解答立体几何问题的一般步骤是:(1)观察图形,建立恰当的空间直角坐标系;(2)写出相应点的坐标,求出相应直线的方向向量;(3)设出相应平面的法向量,利用两直线垂直数量积为零列出方程组求出法向量;(4)将空间位置关系转化为向量关系;(5)根据定理结论求出相应的角和距离.


科目:高中数学 来源: 题型:
【题目】某校高一年级的A,B,C三个班共有学生120人,为调查他们的体育锻炼情况,用分层抽样的方法从这三个班中分别抽取4,5,6名学生进行调查. (Ⅰ)求A,B,C三个班各有学生多少人;
(Ⅱ)记从C班抽取学生的编号依次为C1 , C2 , C3 , C4 , C5 , C6 , 现从这6名学生中随机抽取2名做进一步的数据分析.
(i)列出所有可能抽取的结果;
(ii)设A为事件“编号为C1和C2的2名学生中恰有一人被抽到”,求事件A发生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】命题p:关于x的不等式x2+2ax+4>0对一切x∈R恒成立;命题q:函数f(x)=lagax在(0,+∞)上递增,若p∨q为真,而p∧q为假,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某农场预算用5600元购买单价为50元(每吨)的钾肥和20元(每吨)的氮肥,希望使两种肥料的总数量(吨)尽可能的多,但氮肥数不少于钾肥数,且不多于钾肥数的1.5倍.
(Ⅰ)设买钾肥x吨,买氮肥y吨,按题意列出约束条件、画出可行域,并求钾肥、氮肥各买多少才行?
(Ⅱ)已知A(10,0),O是坐标原点,P(x,y)在(Ⅰ)中的可行域内,求  的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某印刷厂的打印机每5年需淘汰一批旧打印机并购买新机,买新机时,同时购买墨盒,每台新机随机购买第一盒墨150元,优惠0元;再每多买一盒墨都要在原优惠基础上多优惠一元,即第一盒墨没有优惠,第二盒墨优惠一元,第三盒墨优惠2元,……,依此类推,每台新机最多可随新机购买25盒墨.平时购买墨盒按零售每盒200元.
公司根据以往的记录,十台打印机正常工作五年消耗墨盒数如下表:
消耗墨盒数 | 22 | 23 | 24 | 25 |
打印机台数 | 1 | 4 | 4 | 1 |
以这十台打印机消耗墨盒数的频率代替一台打印机消耗墨盒数发生的概率,记ξ表示两台打印机5年消耗的墨盒数.
(1)求ξ的分布列;
(2)若在购买两台新机时,每台机随机购买23盒墨,求这两台打印机正常使用五年在消耗墨盒上所需费用的期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列所给4个图象中,与所给3件事吻合最好的顺序为( )
(1)小明离开家不久,发现自己把作业本忘在家里了,于是立刻返回家里取了作业本再上学;
(2)小明骑着车一路以常速行驶,只是在途中遇到一次交通堵塞,耽搁了一些时间;
(3)小明出发后,心情轻松,缓缓行进,后来为了赶时间开始加速.
A.(4)(1)(2)
B.(4)(2)(3)
C.(4)(1)(3)
D.(1)(2)(4)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com