
已知函数f(x)=ax+x2,g(x)=xln a,a>1.
(1)求证:函数F(x)=f(x)-g(x)在(0,+∞)上单调递增;
(2)若函数y=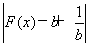 -3有四个零点,求b的取值范围;
-3有四个零点,求b的取值范围;
(3)若对于任意的x1,x2∈[-1,1]时,都有|F(x2)-F(x1)|≤e2-2恒成立,求a的取值范围.
(1)见解析(2)(2- ,0)∪(2+
,0)∪(2+ ,+∞)(3)(1,e2]
,+∞)(3)(1,e2]
【解析】(1)∵F(x)=f(x)-g(x)=ax+x2-xln a,
∴F′(x)=ax·ln a+2x-ln a=(ax-1)ln a+2x.
∵a>1,x>0,∴ax-1>0,ln a>0,2x>0,
∴当x∈(0,+∞)时,F′(x)>0,即函数F(x)在区间(0,+∞)上单调递增.
(2)由(1)知当x∈(-∞,0)时,F′(x)<0,
∴F(x)在(-∞,0)上单调递减,在(0,+∞)上单调递增.
∴F(x)的最小值为F(0)=1.由 -3=0,
-3=0,
得F(x)=b- +3或F(x)=b-
+3或F(x)=b- -3,
-3,
∴要使函数y= -3有四个零点,只需
-3有四个零点,只需
 即b-
即b- >4,即
>4,即 >0,
>0,
解得b>2+ 或2-
或2- <b<0.
<b<0.
故b的取值范围是(2- ,0)∪(2+
,0)∪(2+ ,+∞).
,+∞).
(3)∵?x1,x2∈[-1,1],由(1)知F(x)在(-∞,0)上单调递减,在(0,+∞)上单调递增,
∴F(x)min=F(0)=1.
从而再来比较F(-1)与F(1)的大小即可.
F(-1)= +1+ln a,F(1)=a+1-ln a,
+1+ln a,F(1)=a+1-ln a,
∴F(1)-F(-1)=a- -2ln a.
-2ln a.
令H(x)=x- -2ln x(x>0),
-2ln x(x>0),
则H′(x)=1+ -
- =
= =
= >0,
>0,
∴H(x)在(0,+∞)上单调递增.
∵a>1,∴H(a)>H(1)=0.∴F(1)>F(-1).
∴|F(x2)-F(x1)|的最大值为|F(1)-F(0)|=a-ln a,
∴要使|F(x2)-F(x1)|≤e2-2恒成立,只需a-ln a≤e2-2即可.令h(a)=a-ln a(a>1),h′(a)=1- >0,∴h(a)在(1,+∞)上单调递增.∵h(e2)=e2-2,∴只需h(a)≤h(e2),即1<a≤e2.故a的取值范围是(1,e2]
>0,∴h(a)在(1,+∞)上单调递增.∵h(e2)=e2-2,∴只需h(a)≤h(e2),即1<a≤e2.故a的取值范围是(1,e2]


科目:高中数学 来源:2014年高考数学(文)二轮复习专题提升训练江苏专用阶段检测5练习卷(解析版) 题型:填空题
在圆x2+y2=4所围成的区域内随机取一个点P(x,y),则|x|+|y|≤2的概率为________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮复习专题提升训练江苏专用阶段检测3练习卷(解析版) 题型:填空题
设y=f(x)是一次函数,f(0)=1,且f(1),f(4),f(13)成等比数列,则f(2)+f(4)+…+f(2n)=________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮复习专题提升训练江苏专用阶段检测2练习卷(解析版) 题型:填空题
在△ABC中,若AB=1,AC= |
| +
+ |=|
|=| |,则
|,则 =______.
=______.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮复习专题提升训练江苏专用阶段检测2练习卷(解析版) 题型:填空题
函数y=Asin(ωx+φ)  的图象如图所示,则f(0)=________.
的图象如图所示,则f(0)=________.

查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮复习专题提升训练江苏专用阶段检测1练习卷(解析版) 题型:解答题
已知函数f(x)= .
.
(1)确定y=f(x)在(0,+∞)上的单调性;
(2)若a>0,函数h(x)=xf(x)-x-ax2在(0,2)上有极值,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮复习专题提升训练江苏专用阶段检测1练习卷(解析版) 题型:填空题
若y=f(x)是定义在R上周期为2的周期函数,且f(x)是偶函数,当x∈[0,1]时,f(x)=2x-1,则函数g(x)=f(x)-log3|x|的零点个数为________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮复习专题提升训练江苏专用9练习卷(解析版) 题型:填空题
已知等比数列{an}为递增数列,且a3+a7=3,a2a8=2,则 =________.
=________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮复习专题提升训练江苏专用5练习卷(解析版) 题型:填空题
函数f(x)的定义域是R,f(0)=2,对任意x∈R,f(x)+f′(x)>1,则不等式ex·f(x)>ex+1的解集为______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com