
【题目】已知函数![]() ,
,![]() .
.
(1)求使方程![]() 存在两个实数解时,
存在两个实数解时,![]() 的取值范围;
的取值范围;
(2)设![]() ,函数
,函数![]() ,
,![]() .若对任意
.若对任意![]() ,总存在
,总存在![]() ,使得
,使得![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)求出导函数,可得函数![]() 在区间
在区间![]() 上单调递增,在
上单调递增,在![]() 上单调递减,求得
上单调递减,求得![]() ,
,![]() ,
,![]() ,利用
,利用![]() 可得结果;(2)由(1)知
可得结果;(2)由(1)知![]() ,设
,设![]() 的值域为
的值域为![]() ,因为对任意
,因为对任意![]() ,总存在
,总存在![]() ,使得
,使得![]() ,等价于
,等价于![]() .利用导数研究函数的单调性,求出
.利用导数研究函数的单调性,求出![]() 的值域
的值域![]() ,根据包含关系列不等式求解即可,
,根据包含关系列不等式求解即可,
(1)![]() .
.
令![]() ,得
,得![]() ;令
;令![]() ,得
,得![]() ,
,
所以函数![]() 在区间
在区间![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
所以![]() ,又
,又![]() ,
,![]() ,
,
要使方程![]() 存在两个实数解,则
存在两个实数解,则![]() ,
,
解得![]() .
.
(2)由(1)知![]() ,设
,设![]() 的值域为
的值域为![]() ,因为对任意
,因为对任意![]() ,总存在
,总存在![]() ,使得
,使得![]() ,所以
,所以![]() .
.
因为![]() ,所以
,所以![]() ,
,
当![]() 时,
时,![]() 在
在![]() 上恒成立,所以
上恒成立,所以![]() 在
在![]() 上单调递减,
上单调递减,
又![]() ,不可能满足
,不可能满足![]() .
.
当![]() 时,由于
时,由于![]() ,
,
若![]() ,即
,即![]() ,
,![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
![]() ,又
,又![]() ,
,![]() ,要使
,要使![]() ,则必须有
,则必须有![]() ,化简得
,化简得![]() ,解得
,解得![]() ,又
,又![]() ,所以
,所以![]() .
.
若![]() ,即
,即![]() ,
,![]() 在
在![]() 上单调递减,不可能满足
上单调递减,不可能满足![]() .
.
综上,实数![]() 的取值范围为
的取值范围为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知二次函数![]() 交
交![]() 轴于
轴于![]() 两点(
两点(![]() 不重合),交
不重合),交![]() 轴于
轴于![]() 点. 圆
点. 圆![]() 过
过![]() 三点.下列说法正确的是( )
三点.下列说法正确的是( )
① 圆心![]() 在直线
在直线![]() 上;
上;
② ![]() 的取值范围是
的取值范围是![]() ;
;
③ 圆![]() 半径的最小值为
半径的最小值为![]() ;
;
④ 存在定点![]() ,使得圆
,使得圆![]() 恒过点
恒过点![]() .
.
A. ①②③B. ①③④C. ②③D. ①④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】团体购买公园门票,票价如下表:
购票人数 | 1~50 | 51~100 | 100以上 |
门票价格 | 13元/人 | 11元/人 | 9元/人 |
现某单位要组织其市场部和生产部的员工游览该公园,这两个部门人数分别为a和b![]() ,若按部门作为团体,选择两个不同的时间分别购票游览公园,则共需支付门票费为1290元;若两个部门合在一起作为一个团体,同一时间购票游览公园,则需支付门票费为990元,那么这两个部门的人数
,若按部门作为团体,选择两个不同的时间分别购票游览公园,则共需支付门票费为1290元;若两个部门合在一起作为一个团体,同一时间购票游览公园,则需支付门票费为990元,那么这两个部门的人数![]() ____;
____;![]() ____.
____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学为了组建一支业余足球队,在高一年级随机选取50名男生测量身高,发现被测男生的身高全部在![]() 到
到![]() 之间,将测量结果按如下方式分成六组:第1组
之间,将测量结果按如下方式分成六组:第1组![]() ,第2组
,第2组![]() ,…,第6组
,…,第6组![]() ,如图是按上述分组得到的频率分布直方图,以频率近似概率.
,如图是按上述分组得到的频率分布直方图,以频率近似概率.
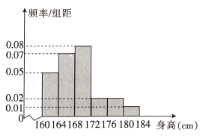
(1)若学校要从中选1名男生担任足球队长,求被选取的男生恰好在第5组或第6组的概率;
(2)试估计该校高一年级全体男生身高的平均数(同一组中的数据用该组区间的中点值代表)与中位数;
(3)现在从第5与第6组男生中选取两名同学担任守门员,求选取的两人中最多有1名男生来自第5组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 过点
过点![]() ,且它的焦距是短轴长的
,且它的焦距是短轴长的![]() 倍.
倍.
(1)求椭圆![]() 的方程.
的方程.
(2)若![]() ,
,![]() 是椭圆
是椭圆![]() 上的两个动点(
上的两个动点(![]() ,
,![]() 两点不关于
两点不关于![]() 轴对称),
轴对称),![]() 为坐标原点,
为坐标原点,![]() ,
,![]() 的斜率分别为
的斜率分别为![]() ,
,![]() ,问是否存在非零常数
,问是否存在非零常数![]() ,使当
,使当![]() 时,
时,![]() 的面积
的面积![]() 为定值?若存在,求
为定值?若存在,求![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() :
:![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,下顶点为
,下顶点为![]() ,椭圆
,椭圆![]() 的离心率是
的离心率是![]() ,
,![]() 的面积是
的面积是![]() .
.
(1)求椭圆![]() 的标准方程.
的标准方程.
(2)直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点(异于
两点(异于![]() 点),若直线
点),若直线![]() 与直线
与直线![]() 的斜率之和为1,证明:直线
的斜率之和为1,证明:直线![]() 恒过定点,并求出该定点的坐标.
恒过定点,并求出该定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义:对于数列![]() ,如果存在常数
,如果存在常数![]() ,使对任意正整数
,使对任意正整数![]() ,总有
,总有![]() 成立,那么我们称数列
成立,那么我们称数列![]() 为“
为“![]() ﹣摆动数列”.
﹣摆动数列”.
①若![]() ,
,![]() ,
,![]() ,则数列
,则数列![]() _____“
_____“![]() ﹣摆动数列”,
﹣摆动数列”,![]() _____“
_____“![]() ﹣摆动数列”(回答是或不是);
﹣摆动数列”(回答是或不是);
②已知“![]() ﹣摆动数列”
﹣摆动数列”![]() 满足
满足![]() ,
,![]() .则常数
.则常数![]() 的值为_____.
的值为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com