
 .
. 时,函数
时,函数 的图象与x轴围成草垛型平面区域,为了估算该区域的面积,采用计算机随机模拟试验,先产生0~2之间的均匀随机数A, 0~1之间的
的图象与x轴围成草垛型平面区域,为了估算该区域的面积,采用计算机随机模拟试验,先产生0~2之间的均匀随机数A, 0~1之间的 均匀随机数B,再判断
均匀随机数B,再判断 是否成立. 我们做2000次试验,得到1273次
是否成立. 我们做2000次试验,得到1273次 ,由此试估算该草垛型平面区域的面积(结果保留两位小数).
,由此试估算该草垛型平面区域的面积(结果保留两位小数).
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 =
= 、Sin
、Sin =-
=-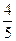 ,则角
,则角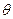 的终边落在直线( )上。
的终边落在直线( )上。| A.7x+24y="0" | B.7x-24y="0" | C.24x+7y="0" | D.24x-7y=0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com