Question

已知f（x）=1-（x-a）（x-b）（a＜b）的两个零点分别是m，n且m＜n，则实数a，b，m，n按从小到大的排列顺序是    ．

Answer 1

【答案】分析：根据零点的定义可知a，b为函数g（x）=（x-a）（x-b）的图象与x轴焦点的横坐标而m，n为f（x）=1-（x-a）（x-b）的零点故可在同一直角坐标系中作出f（x），g（x）的图象即可直观得出a，b，m，n的大小关系．
解答：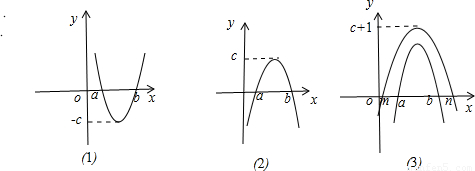
解：令g（x）=（x-a）（x-b）则a，b为函数g（x）的零点如图（1）
∴-g（x）的图象只需将g（x）的图象关于x轴对称即可但-g（x）的零点仍为a，b如图（2）
∴f（x）=1-（x-a）（x-b）的图象只需将-g（x）的图象向上平移一个单位如图（3）根据零点的定义知其图与x轴的交点的横坐标即为f（x）的零点
∴由图（3）易知m＜a＜b＜n
故答案为：m＜a＜b＜n
点评：本题主要考查了利用零点的定义比较零点的大小．关键是要构造函数g（x）=（x-a）（x-b），f（x）=1-（x-a）（x-b）使得a，b，m，n分别为g（x），f（x）的零点再根据图象的变换在同一直角坐标系中作出f（x），g（x）的图象即可比较出a，b，m，n的大小关系，这充分体现了数形结合的思想!