
函数 在
在 上恒为正,则实数
上恒为正,则实数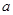 的取值范围是 .
的取值范围是 .
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:高中数学 来源: 题型:
| x2+ax+2 |
| 1 |
| 3 |
| 11 |
| 3 |
查看答案和解析>>
科目:高中数学 来源:江西省上高二中2011-2012学年高一上学期第二次月考数学试题 题型:022
下列说法中正确的是:________.
①函数y=x![]() 的定义域是{x|x≠0};
的定义域是{x|x≠0};
②方程x2+(a-3)x+a=0的有一个正实根,一个负实根,则a<0;
③函数![]() 在定义域上为奇函数;
在定义域上为奇函数;
④函数y=loga(2x-5),(a>0,且a≠1)恒过定点(3,-2);
⑤若3x+3-x=2![]() ,则3x-3-x的值为2
,则3x-3-x的值为2
查看答案和解析>>
科目:高中数学 来源:2011-2012年江西省高一上学期第二次月考数学 题型:填空题
下列说法中正确的是:
① 函数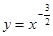 的定义域是
的定义域是 ;
;
② 方程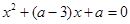 的有一个正实根,一个负实根,则
的有一个正实根,一个负实根,则 ;
;
③ 函数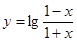 在定义域上为奇函数;
在定义域上为奇函数;
④ 函数 ,
, 恒过定点(3,-2);
恒过定点(3,-2);
⑤ 若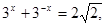 则
则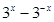 的值为2
的值为2
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
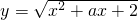 在区间(-∞,1]上是减函数,则实数a∈[-3,-2];
在区间(-∞,1]上是减函数,则实数a∈[-3,-2]; 对称.
对称.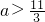 ;
;查看答案和解析>>
科目:高中数学 来源:2011-2012学年江苏省常州中学高三最后冲刺综合练习数学试卷3(文科)(解析版) 题型:解答题
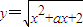 在区间(-∞,1]上是减函数,则实数a∈[-3,-2];
在区间(-∞,1]上是减函数,则实数a∈[-3,-2];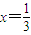 对称.
对称.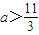 ;
;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com