
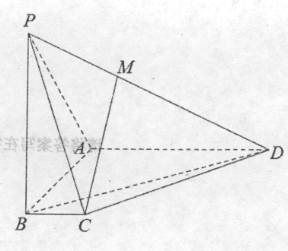
【题目】如图,在四棱锥![]() 中:
中:![]() 底面ABCD,底面ABCD为梯形,
底面ABCD,底面ABCD为梯形,![]() ,
,![]() ,且
,且![]() ,BC=1,M为棱PD上的点。
,BC=1,M为棱PD上的点。
(Ⅰ)若![]() ,求证:
,求证:![]() 平面PAB;
平面PAB;
(Ⅱ)求直线BD与平面PAD所成角的大小;
(Ⅲ)求二面角![]() 的余弦值.
的余弦值.
【答案】(Ⅰ)见解析(Ⅱ)![]() ;(Ⅲ)
;(Ⅲ)![]()
【解析】
(Ⅰ)过点M作MH∥AD,交PA于H,连接BH,证明MH∥BC,CM∥BH,然后证明MC∥平面PAD.(Ⅱ)说明BC⊥AB.PB⊥AB,PB⊥BC,以B为原点,BC,BA,BP所在直线为x,y,z轴建立空间直角坐标系,求平面PAD的一个法向量,则可求出直线BD与平面PAD所成角(Ⅲ)求平面PCD的一个法向量,通过向量的数量积求解二面角![]() 的大小.
的大小.
(Ⅰ)过点M作MH∥AD,交PA于H,连接BH,
∵PM![]() PD,∴ HM
PD,∴ HM![]() AD=BC.
AD=BC.
又MH∥AD,AD∥BC,∴HM∥BC.
∴BCMH为平行四边形,∴CM∥BH.
又BH平面PAB,CM平面PAB,
∴MC∥平面PAB.
(Ⅱ)∵梯形ABCD中,AD∥BC,AD⊥AB,∴BC⊥AB.
∵PB⊥平面ABCD,∴PB⊥AB,PB⊥BC,
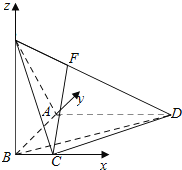
如图,以B为原点,BC,BA,BP所在直线为x,y,z轴建立空间直角坐标系,
∴C(1,0,0),D(3,3,0),A(0,3,0),P(0,0,3).
设平面PAD的一个法向量为![]() (x,y,z),
(x,y,z),
∵![]() (3,3,﹣3),
(3,3,﹣3),![]() (3,0,0)
(3,0,0)
∴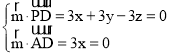 ,
,
取y=1得到![]() (0, 1,1),
(0, 1,1),
设直线BD与平面PAD所成角为![]() ,
,
∴sin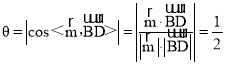 ,
,
∴直线BD与平面PAD所成角的大小为![]() .
.
(Ⅲ)设平面PCD的一个法向量为![]()
![]()
∴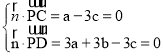 取c=1,得到
取c=1,得到![]()
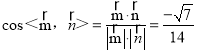 ,
,
∴二面角![]() 的余弦值为
的余弦值为![]()


科目:高中数学 来源: 题型:
【题目】为了检验学习情况,某培训机构于近期举办一场竞赛活动,分别从甲、乙两班各抽取10名学员的成绩进行统计分析,其成绩的茎叶图如图所示(单位:分),假设成绩不低于90分者命名为“优秀学员”.
(1)分别求甲、乙两班学员成绩的平均分(结果保留一位小数);
(2)从甲班4名优秀学员中抽取两人,从乙班2名80分以下的学员中抽取一人,求三人平均分不低于90分的概率.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数![]() 的图像向左平移
的图像向左平移![]() 个单位后得到函数
个单位后得到函数![]() 的图像,且函数
的图像,且函数![]() 满足
满足![]() ,则下列命题中正确的是()
,则下列命题中正确的是()
A. 函数![]() 图像的两条相邻对称轴之间的距离为
图像的两条相邻对称轴之间的距离为![]()
B. 函数![]() 图像关于点
图像关于点![]() 对称
对称
C. 函数![]() 图像关于直线
图像关于直线![]() 对称
对称
D. 函数![]() 在区间
在区间![]() 内为单调递减函数
内为单调递减函数
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙、丙三家企业产品的成本分别为10000,12000,15000,其成本构成如下图所示,则关于这三家企业下列说法错误的是( )
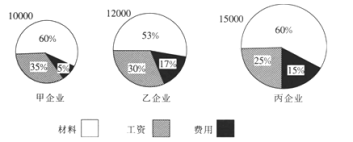
A.成本最大的企业是丙企业B.费用支出最高的企业是丙企业
C.支付工资最少的企业是乙企业D.材料成本最高的企业是丙企业
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() 过点
过点![]() ,且离心率为
,且离心率为![]()
(Ⅰ)求椭圆C的方程;
(Ⅱ)若过原点的直线![]() 与椭圆C交于P、Q两点,且在直线
与椭圆C交于P、Q两点,且在直线![]() 上存在点M,使得
上存在点M,使得![]() 为等边三角形,求直线
为等边三角形,求直线![]() 的方程。
的方程。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com