
【题目】如图1,在边长为2的菱形ABCD中,∠BAD=60°,将△BCD沿对角线BD折起到△B'CD的位置,使平面BC'D⊥平面ABD,E是BD的中点,FA⊥平面ABD,且FA=2 ![]() ,如图2.
,如图2. 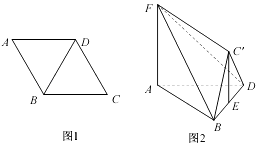
(1)求证:FA∥平面BC'D;
(2)求平面ABD与平面FBC'所成角的余弦值;
(3)在线段AD上是否存在一点M,使得C'M⊥平面FBC?若存在,求 ![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
【答案】
(1)证明:∵BC=CD,E为BD的中点,∴C′E⊥BD,
又平面BC'D⊥平面ABD,且平面BC'D∩平面ABD=BD,
∴C′E⊥ABD,
∵FA⊥平面ABD,∴FA∥C′E,而C′E平面BC'D,FA平面BC'D,
∴FA∥平面BC'D
(2)解:以DB所在直线为x轴,AE所在直线为y轴,EC′所在直线为z轴建立空间直角坐标系,
则B(1,0,0),A(0, ![]() ,0),D(﹣1,0,0),F(0,﹣
,0),D(﹣1,0,0),F(0,﹣ ![]() ,
, ![]() ),
),
C′(0,0, ![]() ),
),
∴ ![]() ,
, ![]() .
.
设平面FBC′的一个法向量为 ![]() ,
,
则 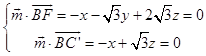 ,取z=1,则
,取z=1,则 ![]() .
.
又平面ABD的一个法向量为 ![]() .
.
∴cos< ![]() >=
>= ![]() =
= ![]() .
.
则平面ABD与平面FBC'所成角的余弦值为 ![]()

(3)解:线段AD上不存点M,使得C'M⊥平面FBC.
假设在线段AD上存在M(x,y,z),使得C'M⊥平面FBC,
设 ![]() ,则(x,y
,则(x,y ![]() ,z)=λ(﹣1,
,z)=λ(﹣1, ![]() ,0)=(﹣λ,
,0)=(﹣λ, ![]() ,0),
,0),
∴x=﹣λ,y= ![]() ,z=0.
,z=0.
则 ![]() =(﹣λ,
=(﹣λ, ![]() ,﹣
,﹣ ![]() ).
).
由 ![]() ,得
,得 ![]() ,即
,即 ![]() 错误.
错误.
∴线段AD上不存点M,使得C'M⊥平面FBC.
【解析】(1)由题意可得C′E⊥BD,又平面BC'D⊥平面ABD,且平面BC'D∩平面ABD=BD,再由面面垂直的性质可得C′E⊥ABD,结合已知可得FA∥C′E,由线面平行的判定可得FA∥平面BC'D;(2)以DB所在直线为x轴,AE所在直线为y轴,EC′所在直线为z轴建立空间直角坐标系,求出所用点的坐标,求得平面FBC′与平面ABD的一个法向量,由两法向量所成角的余弦值可得平面ABD与平面FBC'所成角的余弦值;(3)假设在线段AD上存在M(x,y,z),使得C'M⊥平面FBC,由 ![]() 求得M的坐标,得到
求得M的坐标,得到 ![]() ,由
,由 ![]() 加以判断.
加以判断.
【考点精析】认真审题,首先需要了解直线与平面平行的判定(平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行).


 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(
=( ![]() sinωx,1),
sinωx,1), ![]() =(cosωx,cos2ωx+1),设函数f(x)=
=(cosωx,cos2ωx+1),设函数f(x)= ![]() .
.
(1)若函数f(x)的图象关于直线x= ![]() 对称,且ω∈[0,3]时,求函数f(x)的单调增区间;
对称,且ω∈[0,3]时,求函数f(x)的单调增区间;
(2)在(1)的条件下,当 ![]() 时,函数f(x)有且只有一个零点,求实数b的取值范围.
时,函数f(x)有且只有一个零点,求实数b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】血药浓度(Plasma Concentration)是指药物吸收后在血浆内的总浓度.药物在人体内发挥治疗作用时,该药物的血药浓度应介于最低有效浓度和最低中毒浓度之间.已知成人单次服用1单位某药物后,体内血药浓度及相关信息如图所示: 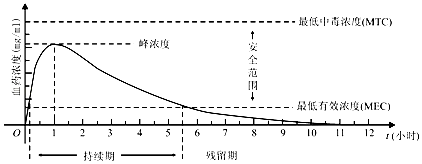
根据图中提供的信息,下列关于成人使用该药物的说法中,不正确的是( )
A.首次服用该药物1单位约10分钟后,药物发挥治疗作用
B.每次服用该药物1单位,两次服药间隔小于2小时,一定会产生药物中毒
C.每间隔5.5小时服用该药物1单位,可使药物持续发挥治疗作用
D.首次服用该药物1单位3小时后,再次服用该药物1单位,不会发生药物中毒
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() ,点P(4,0),过右焦点F作与y轴不垂直的直线l交椭圆C于A,B两点. (Ⅰ)求椭圆C的离心率;
,点P(4,0),过右焦点F作与y轴不垂直的直线l交椭圆C于A,B两点. (Ⅰ)求椭圆C的离心率;
(Ⅱ)求证:以坐标原点O为圆心与PA相切的圆,必与直线PB相切.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正四棱柱ABCD﹣A1B1C1D1中,AB=1,AA1=2,点P是平面A1B1C1D1内的一个动点,则三棱锥P﹣ABC的正视图与俯视图的面积之比的最大值为( ) 
A.1
B.2
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱柱ABCD﹣A1B1C1D1中,侧面ADD1A1⊥底面ABCD,D1A=D1D= ![]() ,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2,O为AD中点.
,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2,O为AD中点.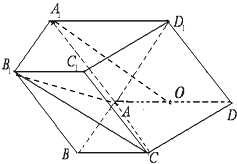
(Ⅰ)求证:A1O∥平面AB1C;
(Ⅱ)求锐二面角A﹣C1D1﹣C的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线C:mx2+ny2=1,(m>0,n<0)的一条渐近线与圆x2+y2﹣6x﹣2y+9=0相切,则双曲线C的离心率等于( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={x|y= ![]() },集合B={x|y=lg(﹣x2﹣7x﹣12)},集合C={x|m+1≤x≤2m﹣1}.
},集合B={x|y=lg(﹣x2﹣7x﹣12)},集合C={x|m+1≤x≤2m﹣1}.
(1)求A∩B;
(2)若A∪C=A,求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com