
如图所示,水渠横断面为等腰梯形.
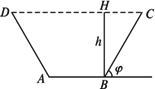
(1)若渠中流水的横断面积为S,水面的高为h,当水渠侧边的倾斜角φ为多大时,才能使横断面被水浸湿的周长为最小?
(2)若被水浸湿的水渠侧边和水渠底面边长都等于a,当水渠侧边倾斜角φ多大时,水流的横断面积为最大?
|
答案:(1)依题意,侧边BC=h·(sinφ)-1,设下底AB=x, 则上底CD=x+2hcotφ, 又S= ∴下底x= ∴横断面被水浸湿周长l= ∴ 令 根据实际问题的意义,当φ= (2)设水渠高为h,水流横断面积为S,则 S= =a2(1+cosφ)·sinφ(0<φ< ∴ 令 故在(0, 最大值为S=a2(1+cos 思路解析:分析各已知条件之间的关系,借助图形的特征,合理选择这些条件间的联系方式,适当选定变元,构造相应的函数关系,通过求导的方法或其他方法求出函数的最小值. |


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:

(1)若渠中流水的横断面积为S,水面的高为h,当水渠侧边的倾斜角Φ为多大时,才能使横断面被水浸湿的周长为最小?
(2)若被水浸湿的水渠侧边和水渠底面边长都等于a,当水渠侧边倾斜角Φ多大时,水流的横断面积为最大?
查看答案和解析>>
科目:高中数学 来源: 题型:

(1)若渠中流水的横断面积为S,水面的高为h,当水渠侧边的倾斜角φ为多大时,才能使横断面被水浸湿的周长为最小?
(2)若被水浸湿的水渠侧边和水渠底面边长都等于a,当水渠侧边倾斜角φ多大时,水流的横断面积为最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
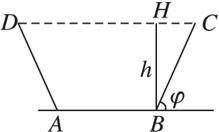
(1)若渠中流水的横断面积为S,水面的高为h,当水渠侧边的倾斜角φ为多大时,才能使横断面被水浸湿的周长为最小?
(2)若被水浸湿的水渠侧边和水渠底面边长都等于a,当水渠侧边倾斜角φ多大时,水流的横断面积为最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com