Question

淮南八公山某种豆腐食品是经过A、B、C三道工序加工而成的，A、B、C工序的产品合格率分别为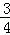、、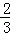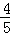．已知每道工序的加工都相互独立，三道工序加工的产品都为合格时产品为一等品；有两次合格为二等品；其它的为废品，不进入市场．

（Ⅰ）正式生产前先试生产2袋食品，求这2袋食品都为废品的概率；

（Ⅱ）设ξ为加工工序中产品合格的次数，求ξ的分布列和数学期望．

 

Answer 1

【答案】

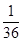(I) ;(II) .

【解析】

试题分析：（Ⅰ） 求出①2袋食品的三道工序都不合格的概率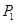，②有一袋食品三道工序都不合格，另一袋有两道工序不合格的概率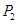，③两袋都有两道工序不合格的概率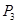，则所求的概率为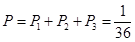;（Ⅱ）由题意可得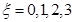，求出离散型随机变量的取每个值的概率，即得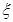的分布列，由分布列求出期望．

试题解析：(I) 2袋食品都为废品的情况为：

①2袋食品的三道工序都不合格；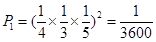

②有一袋食品三道工序都不合格，另一袋有两道工序不合格;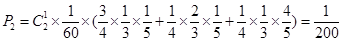

③两袋都有两道工序不合格;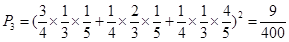

所以2袋食品都为废品的概率为;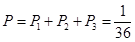

（Ⅱ）由题意可得，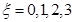

，

，

，

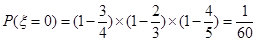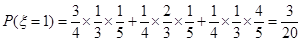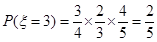故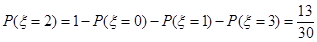P（ξ=2）=1﹣P（ξ=0）﹣P（ξ=1）﹣P（ξ=3）=，得到ξ的分布列如下：

	0	1	2	3

考点：1.相互独立事件的概率乘法公式；2.离散型随机变量及其分布列；3.离散型随机变量的期望与方差．