
分析 设BC=x,根据面积公式用x和sinB表示出三角形的面积,再根据余弦定理用x表示出sinB,代入三角形的面积表达式,进而得到关于x的三角形面积表达式,再根据x的范围求得三角形面积的最大值.
解答 解:设BC=x,则AC=$\sqrt{3}$x,
根据面积公式得S△ABC=$\frac{1}{2}$AB•BCsinB
=$\frac{1}{2}$×2x$\sqrt{1-co{s}^{2}B}$,
根据余弦定理得cosB=$\frac{4+{x}^{2}-3{x}^{2}}{4x}$=$\frac{2-{x}^{2}}{2x}$,
代入上式得S△ABC=$\frac{1}{2}\sqrt{-({x}^{2}-4)^{2}+12}$,
由三角形三边关系有$\left\{\begin{array}{l}{\sqrt{3}x+x>2}\\{x+2>\sqrt{3}x}\end{array}\right.$,
解得$\sqrt{3}$-1<x<$\sqrt{3}$+1.
故当x=2时,S△ABC取得最大值$\sqrt{3}$.
点评 本题主要考查了余弦定理和面积公式在解三角形中的应用.当涉及最值问题时,可考虑用函数的单调性和定义域等问题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (7,-1,4) | B. | (9,1,4) | C. | (3,1,1) | D. | (1,-1,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | -$\frac{3}{2}$ | C. | $\frac{1}{3}$ | D. | -$\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
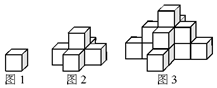 图1是一个水平摆放的小正方体木块,图2,图3是由这样的小正方体木块叠放而成的,按照这样的规律放下去,至第六个叠放的图形中,小正方体木块总数就是( )
图1是一个水平摆放的小正方体木块,图2,图3是由这样的小正方体木块叠放而成的,按照这样的规律放下去,至第六个叠放的图形中,小正方体木块总数就是( )| A. | 25 | B. | 66 | C. | 91 | D. | 120 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2或-1 | B. | 1或2 | C. | ±$\sqrt{3}$或-1 | D. | ±1或2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-$\sqrt{3}$p,0) | B. | (-2$\sqrt{3}$p,0) | C. | (-$\frac{\sqrt{3}p}{3}$,0) | D. | (-$\frac{2\sqrt{3}p}{3}$,0) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com