
如图,已知∠BCD=90°,BC=CD=1,AB⊥平面BCD,∠ADB=60°,E,F分别是AC,AD上的动点,且![]() =
=![]() =λ.
=λ.
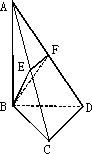
(1)求证:平面BEF⊥平面ABC.
(2)当λ为何值时,平面BEF⊥平面ACD.
|
(1)证明:由AB⊥平面BCD,知AB⊥CD. 又由∠BCD=90°,知CD⊥BC, 所以CD⊥平面ABC. 由 所以EF⊥平面ABC. 因为EF (2)解:由CD⊥平面ABC,知CD⊥BE. 又CD∥EF,所以BE⊥EF. 要使平面BEF⊥平面ACD, 只需BE⊥平面ACD,进而只需满足BE⊥AC. 由BC=CD=1,及∠BCD=90°,得BD= 又∠ADB=60°,及∠ABD=90°,得AB= 在Rt△ABC中,AC= 因为∠ABC=∠AEB=90°,且∠BAC=∠EAB, 所以△ABC∽△AEB,从而 则AE= 故当λ= 点评:线线垂直 |


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:广东省深圳高级中学2012届高三第三次月考数学文科试题 题型:022
(几何证明选讲选做题)
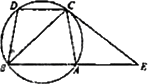
如图:已知AC=BD,过C点的圆的切线与BA的延长线E点,若∠ACE=40°,则∠BCD=________.
查看答案和解析>>
科目:高中数学 来源:2011届湖北省天门市高三模拟考试(一)文科数学 题型:解答题
((本小题满分12分)
如图,已知四棱锥P—ABCD的底面是直角梯形,∠ABC=∠BCD=90o,AB=BC=PB=PC=2CD=2,侧面PBC⊥底面ABCD,O是BC的中点,AO交BD于E.
(1)求证:PA⊥BD;
(2)求二面角P—DC—B的大小.
查看答案和解析>>
科目:高中数学 来源:2010年正定中学高二下学期期末考试数学试题 题型:解答题
(12分)19.(本题满分12分)
如图,已知四面体ABCD中, .
.
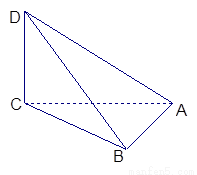
(1)指出与面BCD垂直的面,并加以证明.
(2)若AB=BC=1,CD= ,二面角C-AD-B的平面角为
,二面角C-AD-B的平面角为 ,
, ,求
,求 的表达式及其取值范围.
的表达式及其取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com