（12分）19．（本题满分12分）
如图，已知四面体ABCD中，
．
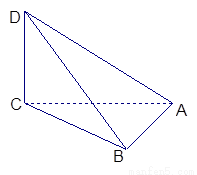
（1）指出与面BCD垂直的面，并加以证明．
（2）若AB＝BC＝1，CD＝
，二面角C－AD－B的平面角为
，
，求
的表达式及其取值范围．
手拉手全优练考卷系列答案科目：高中数学 来源：2011届江西省六校高三联考数学理卷 题型：解答题
（本题满分12分）
对甲、乙两种商品的重量的误差进行抽查，测得数据如下(单位：
)：
甲：13 15 14 14 9 14 21 9 10 11
乙：10 14 9 12 15 14 11 19 22 16
（1）画出样本数据的茎叶图，并指出甲，乙两种商品重量误差的中位数；
（2）计算甲种商品重量误差的样本方差；
（3）现从重量误差不低于15的乙种商品中随机抽取两件，求重量误差为19的商品被抽
中的概率。
查看答案和解析>>
科目：高中数学 来源：2013届福建省高二下学期期中考试文科数学试卷（解析版） 题型：解答题
（本题满分12分）
为了解某年段1000名学生的百米成绩情况，随机抽取了若干学生的百米成绩，成绩全部介于13秒与18秒之间，将成绩按如下方式分成五组：第一组[13，14）；第二组[14，15）;……;第五组[17，18].按上述分组方法得到的频率分布直方图如图所示，已知图中从左到右的前3个组的频率之比为3∶8∶19，且第二组的频数为8.
（1）将频率当作概率，请估计该年段学生中百米成绩在[16，17）内的人数；
（2）求调查中随机抽取了多少个学生的百米成绩；
（3）若从第一、五组中随机取出两个成绩，求这两个成绩的差的绝对值大于1秒的概率.
查看答案和解析>>
科目：高中数学 来源：2011-2012学年安徽省淮北市高三第一次模拟考试文科数学 题型：解答题
（本题满分12分）某工厂有甲、乙两个生产小组，每个小组各有四名工人，某天该厂每位工人的生产情况如下表．
|
|
员工号 |
1 |
2 |
3 |
4 |
|
甲组
|
件数 |
9 |
11 |
1l
|
9
|
|
|
员工号 |
1 |
2 |
3 |
4 |
|
乙组
|
件数 |
b 9 |
8 |
10 |
9 |
(1)用茎叶图表示两组的生产情况；
(2)求乙组员工生产件数的平均数和方差；
(3)分别从甲、乙两组中随机选取一名员工的生产件数，求这两名员工的生产总件数为19的概率．
（注：方差
，其中
为x1，x2，…，xn的平均数）
查看答案和解析>>
科目：高中数学 来源：2010-2011学年江西省六校高三联考数学理卷 题型：解答题
（本题满分12分）
对甲、乙两种商品的重量的误差进行抽查，测得数据如下(单位：
)：
甲：13 15 14 14 9 14 21 9 10 11
乙：10 14 9 12 15 14 11 19 22 16
（1）画出样本数据的茎叶图，并指出甲，乙两种商品重量误差的中位数；
（2）计算甲种商品重量误差的样本方差；
（3）现从重量误差不低于15的乙种商品中随机抽取两件，求重量误差为19的商品被抽
中的概率。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
平面BCD
平面ABD，
面
面BCD，并且面ABC
面BCD。
中作
，M是垂足；在
中作
，E是垂足.
面
平面ABD
.所以
是二面角C-AD-B的平面角.
，
，其取值范围是
