
已知函数f(x)= +ln x.
+ln x.
(1)当a= 时,求f(x)在[1,e]上的最大值和最小值;
时,求f(x)在[1,e]上的最大值和最小值;
(2)若函数g(x)=f(x)- x在[1,e]上为增函数,求正实数a的取值范围.
x在[1,e]上为增函数,求正实数a的取值范围.
(1) 最大值是0,最小值是ln 2-1 (2)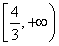
【解析】(1)当a=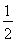 时,f(x)=
时,f(x)=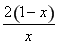 +ln x,
+ln x,
f′(x)=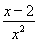 ,令f′(x)=0,得x=2.
,令f′(x)=0,得x=2.
∴当x∈[1,2)时,f′(x)<0,故f(x)在[1,2)上单调递减;
当x∈(2,e]时,f′(x)>0,故f(x)在(2,e]上单调递增.
∴f(x)在区间[1,e]上有唯一的极小值点,
故f(x)min=f(x)极小值=f(2)=ln 2-1.
又∵f(1)=0,f(e)=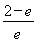 <0.
<0.
∴f(x)在区间[1,e]上的最大值f(x)max=f(1)=0.
综上可知,函数f(x)在[1,e]上的最大值是0,最小值是ln 2-1.
(2)∵g(x)=f(x)-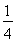 x=
x=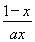 +ln x-
+ln x-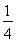 x,
x,
∴g′(x)=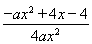 (a>0),
(a>0),
设φ(x)=-ax2+4ax-4,由题意知,只需φ(x)≥0在[1,e]上恒成立即可满足题意.
∵a>0,函数φ(x)的图象的对称轴为x=2,
∴只需φ(1)=3a-4≥0,即a≥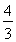 即可.
即可.
故正实数a的取值范围为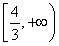 .
.


 应用题作业本系列答案
应用题作业本系列答案科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题3第2课时练习卷(解析版) 题型:填空题
已知数列{an}中,a1=1,an+1=(-1)n(an+1),记Sn为{an}前n项的和,则S2 013=________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题2第2课时练习卷(解析版) 题型:解答题
设函数f(x)=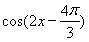 +2cos2x.
+2cos2x.
(1)求f(x)的最大值,并写出使f(x)取最大值时x的集合;
(2)已知△ABC中,角A,B,C的对边分别为a,b,c,若f(B+C)= ,b+c=2,求a的最小值.
,b+c=2,求a的最小值.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题1第6课时练习卷(解析版) 题型:解答题
已知函数f(x)= m(x-1)2-2x+3+ln x,m≥1.
m(x-1)2-2x+3+ln x,m≥1.
(1)当m= 时,求函数f(x)在区间[1,3]上的极小值;
时,求函数f(x)在区间[1,3]上的极小值;
(2)求证:函数f(x)存在单调递减区间[a,b];
(3)是否存在实数m,使曲线C:y=f(x)在点P(1,1)处的切线l与曲线C有且只有一个公共点?若存在,求出实数m的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题1第5课时练习卷(解析版) 题型:选择题
已知f(x)=x3-6x2+9x-abc,a<b<c,且f(a)=f(b)=f(c)=0.现给出如下结论:
①f(0)f(1)>0;②f(0)f(1)<0;③f(0)f(3)>0;
④f(0)f(3)<0.
其中正确结论的序号是( )
A.①③ B.①④
C.②③ D.②④
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题1第4课时练习卷(解析版) 题型:解答题
首届世界低碳经济大会在南昌召开,本届大会以“节能减排,绿色生态”为主题.某单位在国家科研部门的支持下,进行技术攻关,采用了新工艺,把二氧化碳转化为一种可利用的化工产品.已知该单位每月的处理量最少为400吨,最多为600吨,月处理成本y(元)与月处理量x(吨)之间的函数关系可近似地表示为y=x2-200x+80 000,且每处理一吨二氧化碳得到可利用的化工产品价值为100元.
(1)该单位每月处理量为多少吨时,才能使每吨的平均处理成本最低?
(2)该单位每月能否获利?如果获利,求出最大利润;如果不获利,则国家至少需要补贴多少元才能使该单位不亏损?
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题1第3课时练习卷(解析版) 题型:选择题
若定义在R上的偶函数f(x)满足f(x+2)=f(x),且x∈[0,1]时,f(x)=x,则方程f(x)=log3|x|的解有( )
A.2个 B.3个
C.4个 D.多于4个
查看答案和解析>>
科目:高中数学 来源:2014年高考数学理复习方案二轮作业手册新课标·通用版专题四练习卷(解析版) 题型:填空题
在等比数列{an}中,a1+a2=20,a3+a4=40,则a5+a6等于________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com