
已知f(x)=x3-6x2+9x-abc,a<b<c,且f(a)=f(b)=f(c)=0.现给出如下结论:
①f(0)f(1)>0;②f(0)f(1)<0;③f(0)f(3)>0;
④f(0)f(3)<0.
其中正确结论的序号是( )
A.①③ B.①④
C.②③ D.②④
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题3第2课时练习卷(解析版) 题型:选择题
已知数列{an}满足3an+1+an=0,a2=- ,则{an}的前10项和等于( )
,则{an}的前10项和等于( )
A.-6(1-3-10) B. (1-310)
(1-310)
C.3(1-3-10) D.3(1+3-10)
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题2第2课时练习卷(解析版) 题型:填空题
已知直线l:xtan a-y-3tan β=0的斜率为2,在y轴上的截距为1,则tan(α+β)=________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题2第1课时练习卷(解析版) 题型:选择题
若函数y=sin(ωx+φ)(ω>0)的部分图象如图,则ω=( )

A.5 B.4 C.3 D.2
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题1第5课时练习卷(解析版) 题型:解答题
已知函数f(x)= +ln x.
+ln x.
(1)当a= 时,求f(x)在[1,e]上的最大值和最小值;
时,求f(x)在[1,e]上的最大值和最小值;
(2)若函数g(x)=f(x)- x在[1,e]上为增函数,求正实数a的取值范围.
x在[1,e]上为增函数,求正实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题1第5课时练习卷(解析版) 题型:选择题
已知曲线f(x)=ln x在点(x0,f(x0))处的切线经过点(0,-1),则x0的值为( )
A. B.1
B.1
C.e D.10
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题1第4课时练习卷(解析版) 题型:选择题
设正实数x,y,z满足x2-3xy+4y2-z=0,则当 取得最小值时,x+2y-z的最大值为( )
取得最小值时,x+2y-z的最大值为( )
A.0 B.
C.2 D.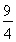
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题1第2课时练习卷(解析版) 题型:解答题
对定义域分别是Df,Dg的函数y=f(x),y=g(x),规定:函数h(x)=
(1)若函数f(x)= ,g(x)=x2,写出函数h(x)的解析式;
,g(x)=x2,写出函数h(x)的解析式;
(2)求问题(1)中函数h(x)的值域.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学理复习方案二轮作业手册新课标·通用版专题四练习卷(解析版) 题型:选择题
已知在等比数列{an}中,有a3a11=4a7,数列{bn}是等差数列,且a7=b7,则b5+b9=( )
A.2 B.4 C.8 D.16
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com