
对定义域分别是Df,Dg的函数y=f(x),y=g(x),规定:函数h(x)=
(1)若函数f(x)= ,g(x)=x2,写出函数h(x)的解析式;
,g(x)=x2,写出函数h(x)的解析式;
(2)求问题(1)中函数h(x)的值域.
(1) h(x)=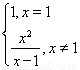 (2) h(x)值域(-∞,0]∪{1}∪[4,+∞)
(2) h(x)值域(-∞,0]∪{1}∪[4,+∞)
【解析】(1)Df={x|x≠1},Dy=R.
当x=1时,h(x)=x2=1;
当x≠1时,h(x)=f(x)g(x)=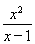 ,
,
∴h(x)=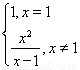
(2)当x=1时,h(1)=1;
当x≠1时,
方法一:h(x)=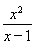 =
=
=x-1+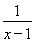 +2;
+2;
当x>1时,h(x)≥4,等号成立条件x=2;
当x<1时,h(x)=-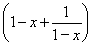 +2≤0,
+2≤0,
等号成立条件x=0,
∴h(x)值域(-∞,0]∪{1}∪[4,+∞).
方法二:y=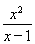 ,x2-yx+y=0.
,x2-yx+y=0.
∵x∈R且x≠1,则关于x的方程有实根,
∴Δ=y2-4y≥0,∴y≥4或y≤0,
∴h(x)值域(-∞,0]∪{1}∪[4,+∞).


 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题2第3课时练习卷(解析版) 题型:选择题
在△ABC中,若∠A=120°, =-1,则|
=-1,则| |的最小值是( )
|的最小值是( )
A. B.2 C.
B.2 C. D.6
D.6
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题1第5课时练习卷(解析版) 题型:选择题
已知f(x)=x3-6x2+9x-abc,a<b<c,且f(a)=f(b)=f(c)=0.现给出如下结论:
①f(0)f(1)>0;②f(0)f(1)<0;③f(0)f(3)>0;
④f(0)f(3)<0.
其中正确结论的序号是( )
A.①③ B.①④
C.②③ D.②④
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题1第4课时练习卷(解析版) 题型:选择题
“0<a<1”是“ax2+2ax+1>0的解集是实数集R”的( )
A.充分而非必要条件 B.必要而非充分条件
C.充要条件 D.既非充分也非必要条件
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题1第3课时练习卷(解析版) 题型:选择题
若定义在R上的偶函数f(x)满足f(x+2)=f(x),且x∈[0,1]时,f(x)=x,则方程f(x)=log3|x|的解有( )
A.2个 B.3个
C.4个 D.多于4个
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题1第2课时练习卷(解析版) 题型:填空题
若函数f(x)=x2-|x+a|为偶函数,则实数a=________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题1第1课时练习卷(解析版) 题型:填空题
已知集合M={1,2,3,4},A⊆M.集合A中所有元素的乘积称为集合A的“累积值”,且规定:当集合A只有一个元素时,其累积值即为该元素的数值,空集的累积值为0.当集合A的累积值是偶数时,这样的集合A共有________个.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题1第1课时练习卷(解析版) 题型:选择题
集合M={3,2a},N={a,b},若M∩N={2},则M∪N=( )
A.{0,1,2} B.{0,1,3}
C.{0,2,3} D.{1,2,3}
查看答案和解析>>
科目:高中数学 来源:2014年高考数学理复习方案二轮作业手册新课标·通用版专题八练习卷(解析版) 题型:选择题
由曲线xy=1,直线y=x,y=3所围成的平面图形的面积为( )
A.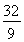 B.2-ln 3 C.4+ln 3 D.4-ln 3
B.2-ln 3 C.4+ln 3 D.4-ln 3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com