
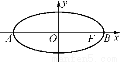
如图,在平面直角坐标系xOy中,已知椭圆 =1的左、右顶点为A、B,右焦点为F.设过点T(t,m)的直线TA、TB与椭圆分别交于点M(x1,y1)、N(x2,y2),其中m>0,y1>0,y2<0.
=1的左、右顶点为A、B,右焦点为F.设过点T(t,m)的直线TA、TB与椭圆分别交于点M(x1,y1)、N(x2,y2),其中m>0,y1>0,y2<0.
(1)设动点P满足PF2-PB2=4,求点P的轨迹;
(2)设x1=2,x2= ,求点T的坐标;
,求点T的坐标;
(3)设t=9,求证:直线MN必过x轴上的一定点(其坐标与m无关).
(1)x= (2)
(2)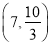 (3)见解析
(3)见解析
【解析】(1)【解析】
设点P(x,y),则F(2,0)、B(3,0)、A(-3,0).由PF2-PB2=4,得(x-2)2+y2-[(x-3)2+y2]=4,化简得x=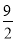 ,故所求点P的轨迹为直线x=
,故所求点P的轨迹为直线x= .
.
(2)【解析】
将x1=2,x2=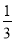 分别代入椭圆方程,以及y1>0,y2<0得M
分别代入椭圆方程,以及y1>0,y2<0得M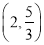 、N
、N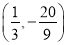 .直线MTA的方程为
.直线MTA的方程为 ,即y=
,即y=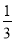 x+1.直线NTB的方程为
x+1.直线NTB的方程为 ,即y=
,即y=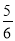 x-
x-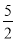 .联立方程组,解得
.联立方程组,解得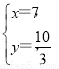 所以点T的坐标为
所以点T的坐标为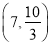 .
.
(3)证明:点T的坐标为(9,m),直线MTA的方程为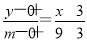 ,即y=
,即y=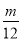 (x+3).直线NTB的方程为
(x+3).直线NTB的方程为 ,即y=
,即y=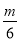 (x-3).
(x-3).
分别与椭圆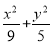 =1联立方程组,同时考虑到x1≠-3,x2≠3,解得
=1联立方程组,同时考虑到x1≠-3,x2≠3,解得
M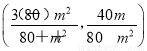 、N
、N
(证法1)当x1≠x2时,直线MN的方程为 ,令y=0,解得x=1,此时必过点D(1,0);当x1=x2时,直线MN的方程为x=1,与x轴交点为D(1,0),所以直线MN必过x轴上的一定点D(1,0).
,令y=0,解得x=1,此时必过点D(1,0);当x1=x2时,直线MN的方程为x=1,与x轴交点为D(1,0),所以直线MN必过x轴上的一定点D(1,0).
(证法2)若x1=x2,则由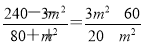 及m>0,得m=2
及m>0,得m=2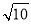 ,此时直线MN的方程为x=1,
,此时直线MN的方程为x=1,

过点D(1,0).若x1≠x2,则m≠2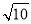 .直线MD的斜率kMD=
.直线MD的斜率kMD= ,
,
直线ND的斜率kND= ,得kMD=kND,所以直线MN过D点.
,得kMD=kND,所以直线MN过D点.
因此,直线MN必过x轴上的点D(1,0).


科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第九章第4课时练习卷(解析版) 题型:解答题
如图,已知直角坐标平面上点Q(2,0)和圆C:x2+y2=1,动点M到圆C的切线长与|MQ|的比等于 .求动点M的轨迹方程,并说明它表示什么.
.求动点M的轨迹方程,并说明它表示什么.

查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第九章第11课时练习卷(解析版) 题型:解答题
已知椭圆E: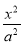 +y2=1(a>1)的上顶点为M(0,1),两条过M的动弦MA、MB满足MA⊥MB.
+y2=1(a>1)的上顶点为M(0,1),两条过M的动弦MA、MB满足MA⊥MB.
(1)当坐标原点到椭圆E的准线距离最短时,求椭圆E的方程;
(2)若Rt△MAB面积的最大值为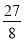 ,求a;
,求a;
(3)对于给定的实数a(a>1),动直线AB是否经过一定点?如果经过,求出定点坐标(用a表示);反之,说明理由.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第九章第11课时练习卷(解析版) 题型:填空题
以双曲线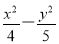 =1的中心为顶点,且以该双曲线的右焦点为焦点的拋物线方程是__________.
=1的中心为顶点,且以该双曲线的右焦点为焦点的拋物线方程是__________.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第九章第10课时练习卷(解析版) 题型:解答题
如图,在平面直角坐标系xOy中,圆C:(x+1)2+y2=16,点F(1,0),E是圆C上的一个动点,EF的垂直平分线PQ与CE交于点B,与EF交于点D.

(1)求点B的轨迹方程;
(2)当点D位于y轴的正半轴上时,求直线PQ的方程;
(3)若G是圆C上的另一个动点,且满足FG⊥FE,记线段EG的中点为M,试判断线段OM的长度是否为定值?若是,求出该定值;若不是,说明理由.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第九章第10课时练习卷(解析版) 题型:填空题
已知双曲线E的中心为原点,F(3,0)是E的焦点,过F的直线l与E相交于A、B两点,且AB的中点为N(-12,-15),则E的方程为____________.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年陕西西工大附中高三上学期第四次适应性训练理数学卷(解析版) 题型:解答题
如图,四边形ABCD为正方形,PD⊥平面ABCD,PD∥QA,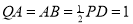 .
.

(1)证明:平面PQC⊥平面DCQ;
(2)求二面角Q—BP—C的余弦值.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年陕西西工大附中高三上学期第四次适应性训练理数学卷(解析版) 题型:选择题
设 ,则使函数
,则使函数 的定义域为R且为奇函数的所有
的定义域为R且为奇函数的所有 的值有( )
的值有( )
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:高中数学 来源:2013-2014学年陕西西安铁一中国际合作学校高三下第一次模拟考试理科数学试卷(解析版) 题型:选择题
函数 (
(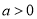 ,且
,且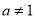 )的图像过一个定点,则这个定点坐标是( )
)的图像过一个定点,则这个定点坐标是( )
A.(5,1) B.(1,5) C.(1,4) D.(4,1)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com