
分析 (1)利用所给数据,即可画出甲、乙两位学生成绩的茎叶图,指出学生甲成绩的中位数和学生乙成绩的众数;
(2)根据乙的数据,求学生乙成绩的平均数和方差;
(3)从甲同学超过80分的6个成绩中任取两个,基本事件共15个,至少有一次超过90分的基本事件,共9个,即可求这两个成绩中至少有一个超过90分的概率.
解答 解:(1)茎叶图如下: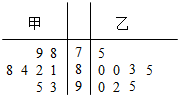 …(2分)
…(2分)
学生甲成绩中位数为83,学生乙成绩众数为8;…(4分)
(2)$\overline{x_乙}=\frac{1}{8}(75+80×2+83+85+90+92+95)$=85,…(6分)
∴${{S}_{乙}}^{2}$=$\frac{1}{8}$[(75-85)2+(80-85)2+(80-85)2+(83-85)2+(85-85)2+(90-85)2+(92-85)2+(95-85)2]=41;…(8分)
(3)甲同学超过80分的成绩有82 81 95 88 93 84,
任取两次成绩,所有基本事件为:(82,81),(82,95),(82,88),(82,93),(82,84),(81,95),(81,88),(81,93),(81,84),(95,88),(95,93),(95,84),(88,93),(88,84),(93,84)共15个.…(10分)
其中至少有一次超过90分的基本事件为:(82,95)(82,93)(81,95)(81,93)(95,88),(95,93),(95,84),(88,93)(93,84)共9个.…(11分)
∴这两次成绩中至少有一次超过90分的概率为$\frac{9}{15}=\frac{3}{5}$.…(12分)
点评 本题考查茎叶图,考查概率的计算,考查学生分析解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
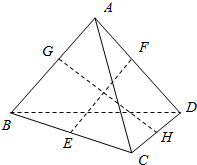 已知:正四面体ABCD(所有棱长均相等)的棱长为1,E、F、G、H分别是四面体ABCD中各棱的中点,设:$\overrightarrow{AB}=\overrightarrow a,\overrightarrow{AC}=\overrightarrow b,\overrightarrow{AD}=\overrightarrow c$,试采用向量法解决下列问题
已知:正四面体ABCD(所有棱长均相等)的棱长为1,E、F、G、H分别是四面体ABCD中各棱的中点,设:$\overrightarrow{AB}=\overrightarrow a,\overrightarrow{AC}=\overrightarrow b,\overrightarrow{AD}=\overrightarrow c$,试采用向量法解决下列问题查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{7}{4}$,+∞) | B. | (一∞,$\frac{7}{4}$) | C. | (0,$\frac{7}{4}$) | D. | ($\frac{7}{4}$,2) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com