
方案一:等速螺线,如图2-4-6中图(1).图中画出了关于点O对称的两支蚊香是沿这两支曲线剪开的平面部分(以下同).
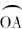
图2-4-6
方案二:圆的渐开线,如图2-4-6(2).图中曲线![]() 是圆弧,曲线
是圆弧,曲线![]() 是圆的渐开线(以下同).
是圆的渐开线(以下同).
受方案二的启示,可得.
方案三:正方形的渐开线,如图2-4-6(3).
请根据图(2)和图(3)写出图(2)和图(3)对应曲线的方程.
思路分析:本探究目的在于探讨数学的美在实际问题中的体现.要写出相应曲线的方程,可以根据曲线满足的条件,可以使用参数方程,普通方程或者极坐标方程写出,关键在于对知识的灵活掌握和应用.首先要明白渐开线的含义,可以根据课本中圆的渐开线的定义和求解的方法进行类比.建立适当的坐标系,根据条件写出坐标满足的关系式.
解:在方案二中,建立如题图中图(2)所示的直角坐标系,圆弧![]() 的参数方程为
的参数方程为
![]()
(取基圆的半径r=1,![]() ≤φ<1).
≤φ<1).
曲线![]() 的参数方程为
的参数方程为![]() (φ为参数,且φ≥1).
(φ为参数,且φ≥1).
在方案三中,曲线是由圆弧与圆弧内连结的,建立如题图中图(3)所示的直角坐标系,设OA=OC=1,则曲线![]() 的各段由下列方程构成(式中n∈N,以下同):
的各段由下列方程构成(式中n∈N,以下同):
(x-![]() )2+(y-
)2+(y-![]() )2=
)2=![]() (0≤x<1,
(0≤x<1,![]() ≤y<0);
≤y<0);
x2+(y-1)2=2(4n-3)2,〔4n-3≤x<![]() (4n-3),-4n+4≤y<4n-2〕;
(4n-3),-4n+4≤y<4n-2〕;
(x+1)2+y2=2(4n-2)2〔-4n+1≤x<4n-3,4n-2≤y<![]() (4n-2)〕;
(4n-2)〕;
x2+(y+1)2=2(4n-1)2〔-![]() (4n-1)≤x<-4n+1,-4n≤y<4n-2〕;
(4n-1)≤x<-4n+1,-4n≤y<4n-2〕;
(x-1)2+y2=2(4n)2〔-4n+1≤x<4n+1,-4![]() n≤y<-4n〕.
n≤y<-4n〕.


科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| f(x2)-f(x1) |
| x2-x1 |
| f(b)-f(a) |
| b-a |
| b-a |
| b |
| b |
| a |
| b-a |
| a |
查看答案和解析>>
科目:高中数学 来源:2011-2012学年四川省高三2月月考理科数学 题型:解答题
盒中装有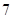 个零件,其中
个零件,其中 个是使用过的,另外
个是使用过的,另外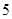 个未经使用.
个未经使用.
(Ⅰ)从盒中每次随机抽取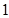 个零件,每次观察后都将零件放回盒中,求
个零件,每次观察后都将零件放回盒中,求 次抽取中恰有
次抽取中恰有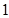 次
次
抽到使用过的零件的概率;
(Ⅱ)从盒中随机抽取 个零件,使用后放回盒中,记此时盒中使用过的零件个数为
个零件,使用后放回盒中,记此时盒中使用过的零件个数为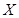 ,求
,求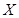 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com