
分析 直线x+ay-1=0与2x-y+5=0垂直,利用相互垂直的直线斜率之间的关系可得a.则二项式(ax2-$\frac{1}{x}$)5化为$(2{x}^{2}-\frac{1}{x})^{5}$,可得Tr+1=${∁}_{5}^{r}$(2x2)r$(-\frac{1}{x})^{5-r}$=(-1)5-r2r${∁}_{5}^{r}$x3r-5.
令3r-5=4,解得r即可得出.
解答 解:∵直线x+ay-1=0与2x-y+5=0垂直,
∴-$\frac{1}{a}$×2=-1,
解得a=2.
则二项式(ax2-$\frac{1}{x}$)5化为$(2{x}^{2}-\frac{1}{x})^{5}$,
∴Tr+1=${∁}_{5}^{r}$(2x2)r$(-\frac{1}{x})^{5-r}$=(-1)5-r2r${∁}_{5}^{r}$x3r-5.
令3r-5=4,解得r=3.
∴T4=8${∁}_{5}^{3}$•x4=80x4.
∴展开式中x4的系数为80.
故答案为:80.
点评 本题考查了相互垂直的直线斜率之间的关系、二项式定理的应用,考查了推理能力与计算能力,属于中档题.


 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
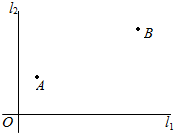 如图,在A,B两城周边有两条直线互相垂直的高速公路l1,l2,在点O外交汇,A城到高速公路l1,l2的距离分别是30km,20km,B城到高速公路l1,l2的距离分别是60km,80km,为了方便居民出行,现要在高速公路l1或l2上建造一个高速公路出入口P(不能建造在点O处),经调查,若出入口O建造在高速公路l1上,A,B两城居民的“不满意度”M1=$\frac{1}{2}$(PA+PB),若出入口P建造在高速公路l2上,A,B两城居民的“不满意度”M2=$\frac{1}{2}$$\sqrt{P{A}^{2}+P{B}^{2}}$.
如图,在A,B两城周边有两条直线互相垂直的高速公路l1,l2,在点O外交汇,A城到高速公路l1,l2的距离分别是30km,20km,B城到高速公路l1,l2的距离分别是60km,80km,为了方便居民出行,现要在高速公路l1或l2上建造一个高速公路出入口P(不能建造在点O处),经调查,若出入口O建造在高速公路l1上,A,B两城居民的“不满意度”M1=$\frac{1}{2}$(PA+PB),若出入口P建造在高速公路l2上,A,B两城居民的“不满意度”M2=$\frac{1}{2}$$\sqrt{P{A}^{2}+P{B}^{2}}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{7}$ | B. | $\frac{4}{7}$ | C. | $\frac{1}{3}$ | D. | $\frac{8}{21}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 每吨产品 | 煤(吨) | 水(吨) | 电(千瓦) |
| A | |||
| B |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{7}$ | B. | $\frac{3}{7}$ | C. | $\frac{4}{7}$ | D. | $\frac{5}{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 直角三角形 | B. | 等腰三角形 | ||
| C. | 等腰直角三角形 | D. | 等腰或直角三角形 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{5}{12}$ | B. | $\frac{5}{12}$ | C. | -$\frac{12}{5}$ | D. | $\frac{12}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com